定義
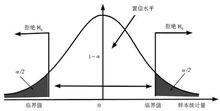 假設檢驗
假設檢驗在統計學中,零假設(虛無假設)是做統計檢驗時的一類假設。零假設的內容一般是希望證明其錯誤的假設。比如說,在相關性檢驗中,一般會取“兩者之間沒有關聯”作為零假設,而在獨立性檢驗中,一般會取“兩者之間有關聯”作為零假設。與零假設相對的是備擇假設(對立假設),即不希望看到的另一種可能。從數學上來看,零假設和備擇假設的地位是相等的,但是在統計學的實際運用中,常常需要強調一類假設為應當或期望實現的假設。如果一個統計檢驗的結果拒絕零假設(結論不支持零假設),而實際上真實的情況屬於零假設,那么稱這個檢驗犯了第一類錯誤。反之,如果檢驗結果支持零假設,而實際上真實的情況屬於備擇假設,那么稱這個檢驗犯了第二類錯誤。通常的做法是,在保持第一類錯誤出現的機會在某個特定水平上的時候,儘量減少第二類錯誤出現的機率。
確定標準編輯
1、零假設一般是有意推翻的假設;
2、由於第一類錯誤的機率可以通過顯著性水平的選定加以控制,零假設一般是如果出現第一類錯誤後後果更為嚴重的情況的假設。
套用
比如我要做一些實驗證明陽光對植物的影響,我是希望發現陽光與植物是有一些關係的,這種情況下我做原假設/零假設即是:陽光對植物沒有影響。備擇假設:陽光對植物有影響。
第一類錯誤:“棄真”,零假設為真,卻拒絕了零假設。(即小機率事件(某些植物跟陽光無關)發生的可能性,當它在5%左右,可以拒絕零假設。)
第二類錯誤:“取偽”,零假設為假,卻接受了零假設。(實際上植物和陽光有關係,然而我們忽略掉了它們的關係,睜一隻眼閉一隻眼接受了。)

