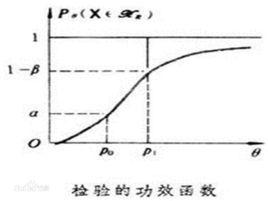
簡介
參數檢驗,是數理統計學中根據一定假設條件由樣本推斷總體的一種方法。具體作法是:根據問題的需要對所研究的總體作某種假設,記作H0;選取合適的統計量,這個統計量的選取要使得在假設H0成立時,其分布為已知;由實測的樣本,計算出統計量的值,並根據預先給定的顯著性水平進行檢驗,作出拒絕或接受假設H0的判斷。常用的假設檢驗方法有U檢驗法、T檢驗法、χ2檢驗法(卡方檢驗)、F檢驗法等。
參數假設檢驗又稱統計假設檢驗,是一種基本的統計推斷形式,也是數理統計學的一個重要的分支,用來判斷樣本與樣本,樣本與總體的差異是由抽樣誤差引起還是本質差別造成的統計推斷方法。其基本原理是先對總體的特徵作出某種假設,然後通過抽樣研究的統計推理,對此假設應該被拒絕還是接受作出推斷。
基本思想
參數假設檢驗的基本思想是小機率反證法思想。小機率思想是指小機率事件(P<0.01或P<0.05)在一次試驗中基本上不會發生。反證法思想是先提出假設(檢驗假設H0),再用適當的統計方法確定假設成立的可能性大小,如可能性小,則認為假設不成立,若可能性大,則還不能認為不假設成立。
假設是否正確,要用從總體中抽出的樣本進行檢驗,與此有關的理論和方法,構成假設檢驗的內容。設A是關於總體分布的一項命題,所有使命題A成立的總體分布構成一個集合H0,稱為原假設(常簡稱假設)。使命題A不成立的所有總體分布構成另一個集合H1,稱為備擇假設。如果H0可以通過有限個實參數來描述,則稱為參數假設,否則稱為非參數假設(見非參數統計)。如果H0(或H1)只包含一個分布,則稱原假設(或備擇假設)為簡單假設,否則為複合假設。對一個假設H0進行檢驗,就是要制定一個規則,使得有了樣本以後,根據這規則可以決定是接受它(承認命題A正確),還是拒絕它(否認命題A正確)。這樣,所有可能的樣本所組成的空間(稱樣本空間)被劃分為兩部分HA和HR(HA的補集),當樣本x∈HA時,接受假設h0;當x∈HR時,拒絕H0。集合HR常稱為檢驗的拒絕域,HA稱為接受域。因此選定一個檢驗法,也就是選定一個拒絕域,故常把檢驗法本身與拒絕域HR等同起來。
參數檢驗運用範圍
當總體分布已知(如總體為常態分配),根據樣本數據對總體分布的統計參數進行推斷。
此時,總體的分布形式是給定的或是假定的,只是其中一些參數的取值或範圍未知,分析的主要目的是估計參數的取值,或對其進行某種統計檢驗。這類問題往往用參數檢驗來進行統計推斷。它不僅僅能夠對總體的特徵參數進行推斷,還能夠實現兩個或多個總體的參數進行比較。
參數檢驗的步驟
1、提出檢驗假設又稱無效假設,符號是H0;備擇假設的符號是H1。
H0:樣本與總體或樣本與樣本間的差異是由抽樣誤差引起的;
H1:樣本與總體或樣本與樣本間存在本質差異;
預先設定的檢驗水準為0.05;當檢驗假設為真,但被錯誤地拒絕的機率,記作α,通常取α=0.05或α=0.01。
2、選定統計方法,由樣本觀察值按相應的公式計算出統計量的大小,如X2值、t值等。根據資料的類型和特點,可分別選用Z檢驗,T檢驗,秩和檢驗和卡方檢驗等。
3、根據統計量的大小及其分布確定檢驗假設成立的可能性P的大小並判斷結果。若P>α,結論為按α所取水準不顯著,不拒絕H0,即認為差別很可能是由於抽樣誤差造成的,在統計上不成立;如果P≤α,結論為按所取α水準顯著,拒絕H0,接受H1,則認為此差別不大可能僅由抽樣誤差所致,很可能是實驗因素不同造成的,故在統計上成立。P值的大小一般可通過查閱相應的界值表得到。
教學中的做法:
1.根據實際情況提出原假設和備擇假設;
2.根據假設的特徵,選擇合適的檢驗統計量;
3.根據樣本觀察值,計算檢驗統計量的觀察值(obs);
4.選擇許容顯著性水平,並根據相應的統計量的統計分布表查出相應的臨界值(ctrit);
5.根據檢驗統計量觀察值的位置決定原假設取捨。