簡介
 信號流圖
信號流圖由美國麻省理工學院的梅森(Mason)於20世紀50年代首先提出;
套用於:反饋系統分析、線性方程組求解、線性系統模擬及數字濾波器設計等方面。
實際上是用一些點和支路來描述系統:
線段表示信號傳輸的路徑,稱為支路。支路表示了一個信號與另一信號的函式關係,
信號只能沿著支路上的箭頭方向通過。
信號的傳輸方向用箭頭表示,轉移函式標在箭頭附近,相當於乘法器。結點可以把所有輸入支路的信號疊加,並把總和信號傳送到所有輸出支路。
詳細說明
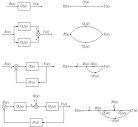
 信號流圖
信號流圖對於複雜的系統,方框圖的簡化過程是冗長的。梅森(S.J.Mason)提出了一種信號流圖法,可以不需要經過任何簡化,直接確定系統輸入和輸出變數間的聯繫,再利用梅森公式求出系統的傳遞函式。
信號流圖及其術語
與圖3.55所示系統方框圖對應的系統信號流圖如圖3.56所示。由圖可以看出,信號流圖中的網路是由一些定向線段將一些節點連線起來組成的。下面說明這些線段和節點的含義。
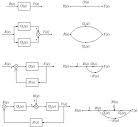
(1)節點 表示變數或信號,其值等於所有進入該節點的信號之和。例如:
是圖3.56中的節點。
(2)輸入節點 它是只有輸出的節點,也稱源點。例如,圖3.56中 是一個輸入節
 信號流圖
信號流圖點。(3)輸出節點 它是只有輸入的節點,也稱匯點。然而這個條件並不總是能滿足的。為了滿足定義的要求可引進增益為1的線段。例如,圖3.56中右端點 為輸出節點。
(4)混和節點 它是既有輸入又有輸出的節點。例如,圖3.56中 是一個混和節點。
(5)支路 定向線段稱為支路,其上的箭頭表明信號的流向,各支路上還標明了增益,即支路的傳遞函式。例如,圖3.56中從節點 到 為一支路,其中 為該支路的
 信號流圖
信號流圖增益。(6)通路 沿支路箭頭方向穿過各相連支路的路徑稱為通路。
(7)前向通道 從輸入節點到輸出節點的通路上通過任何節點不多於一次的通路稱為前向通道。例如,圖3.56中的 — — 是前向通道。
(8)迴路 始端與終端重合且與任何節點相交不多於一次的通道稱為迴路。例如,圖3.56中 — — 是一條迴路。
(9)不接觸迴路 沒有任何公共節點的迴路稱為不接觸迴路。
信號流圖的繪製
繪製系統的信號流圖,首先必須將描述系統的線性微分方程變換成以 為變數的
 信號流圖
信號流圖代數方程;其次,線性代數方程組中每一個方程都要寫成因果關係式。且在書寫時,將作為“因”的一些變數寫在等式右端,而把“果”的變數寫在等式左端。 下面以圖3.57所示的二級 電路網路為例說明信號流圖的繪製步驟。
對於由兩個環節(這裡是兩個 電路)串聯而成的系統,由於後一環節的存在,影響前一環節的輸出,因此兩相鄰環節間存在著負載效應。這時必須將它們視為一個整體來考慮。所以,根據基爾霍夫定律,可寫出下列原始方程將以上各式作拉氏變換,得方程組。