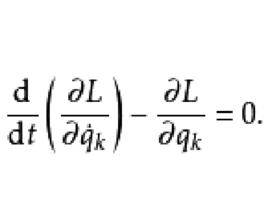基本介紹
在功的表達式
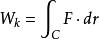保守系中，我們希望搞清楚這個積分能否不與積分路線相關。若這個系統是保守的，這就可能，一個力場被稱為保守力場的條件是：
保守系(1)只是作用位置的函式，即
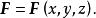保守系
保守系 保守系 保守系(2) 存在一個這樣的標量函式，它使可以作為函式的梯度來求得，即
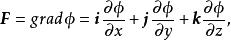保守系由此，保守力所作的功成為
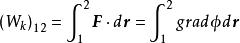保守系
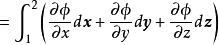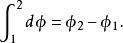保守系
保守系如果在積分號下的被積函式是恰當微分，則所作的功 與 路線無關，而只取決於始末端點。上列等式表明，當力是保守力時，情況就是這樣的。對於閉合迴路
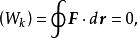保守系也就是說，所作的功為零 。
保守系的拉格朗日方程
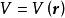保守系
保守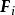系
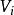保守系保守系統中必存在著勢能V，是坐標的函式，記作。而每個保守力都有一個相應的勢能，兩者的關係為
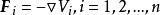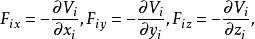保守系
保守系系統的勢能就是所有的保守力共同具有的，所以有
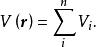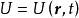保守系
保守系同理，對於有勢系統，有勢力也有一個相應的位置能量，表示為，稱為 勢函式。
顯然，勢能和勢函式的區別在於是否與時間有關。我們將保守系看成是有勢系的特殊情況，適應於保守系統的拉格朗日方程也適應於有勢系的拉格朗日方程。
保守系統的廣義力按定義式可以求得
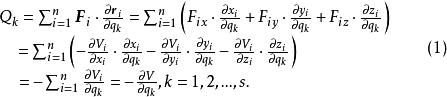保守系這樣基本形式的拉格朗日方程可改寫為
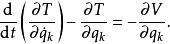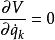保守系
保守系由於V中一般不包含廣義速度，即，所以，方程可寫成
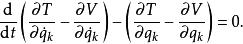保守系令
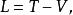保守系所以基本形式的拉格朗日方程改寫成
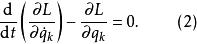保守系
保守系式(2)為 保守系的拉格朗日方程，稱為 拉格朗日函式，顯然它具有能量的量綱。與系統的動能必須用系統的廣義坐標表示一樣，這裡，無論是系統的勢能還是勢函式必須表示成廣義坐標的函式 。
保守系在廣義坐標中的平衡方程
通過虛功原理知道，分析力學中用廣義坐標表示的系統平衡條件是所有的廣義力在任意虛位移下所做的虛功之和為零，即
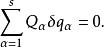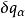保守系
保守系因為諸是相互獨立的，因而得出廣義坐標表示的平衡方程是所有的廣義力為零，即
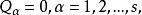保守系如果作用在系統上的力全是保守力，由式(1)知
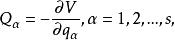保守系式中V為系統的勢能。故保守系統平衡的條件是勢能具有穩定值，即
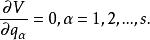保守系保守系的哈密頓函式
如果系統為保守系，則哈密頓函式可用來表示此系統的總能量(動能和勢能)，即
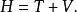保守系這為建立系統的哈密頓函式提供了簡易的方法 。
