基本定理
積分形式的動能定理
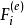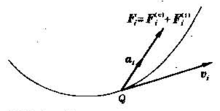
動能定理設質點系中任一質點的質量為m，受外力的合力
和內力
的合力作用，加速度為
，沿曲線軌跡運動到Q點時的速度為
（見圖）。
動能定理根據牛頓第二定律，有：
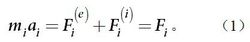動能定理將式（1）向軌跡的切線方向投影，得式
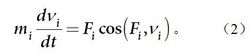動能定理因
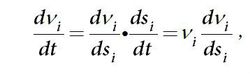動能定理，
代入式（2）可得：
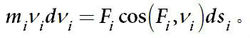動能定理。
上式可以改寫為：
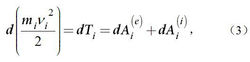動能定理式中為質點i的動能；和分別為質點i上外力和內力的元功。對於整個質點系則應為：
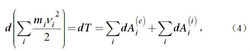動能定理式中為質點系的總動能。對式（4）進行積分，可得：
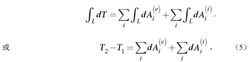動能定理式中T1，為質點系在過程開始時的動能；T2為質點系在過程結束時的動能。
式（5）是以積分形式表示的質點系的動能定理，它表明:質點系的總動能在某個力學過程中的改變數，等於質點系所受的諸外力和諸內力在此過程中所做功的總和。
微分形式的動能定理
將式（4）兩邊除以dt，得：
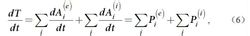動能定理
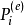動能定理式中
為外力的功率；
為內力的功率。
式（6）是以微分形式表示的質點系的動能定理，它表明；質點系的總動能隨時間的變化率等於質點系所受諸外力和諸內力在單位時間內所作功的總和。
質點是質點系的一個特殊情況，故動能定理也適用於質點。但是，對於質點和剛體，諸內力所做功的總和等於零，因為前者根本不受內力作用，而後者的內力則成對出現，其大小相等，方向相反，作用在同一直線上，且剛體上任兩點的距離保持不變，故其內力作功總和等於零。
定理2
內容
質點系所有外力做功之和加上所有內力做功之和等於質點系總動能的改變數。
和質點動能定理一樣，質點系動能定理只適用於慣性系，因為外力對質點系做功與參照系選擇有關，而內力做功卻與選擇的參照系無關，因為力總是成對出現的，一對作用力和反作用力（內力）所做功代數和取決於相對位移，而相對位移與選擇的參照系無關。
動能定理的內容：所有外力對物體總功，（也叫做合外力的功）等於物體的動能的變化。
牛頓第二定律只適用於巨觀低速的情況，因為在相對論中m是不成立的
，質量隨速度改變。而動量定理可適用於世界上任何情況。
物體由於運動而具有的能量. 用E表示。
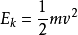動能定理表達式：
，動能是標量 也是狀態量。
單位：焦耳(J) 1kg·m/s = 1J
(2) 動能定理內容:合外力做的功等於物體動能的變化。
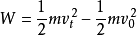動能定理表達式：
適用範圍
恆力做功、變力做功、分段做功、全程做功等均可適用。
動量定理與動能定理的區別
動量定理Ft=mv-mv反映了力對時間的累積效應，是力在時間上的積分。
動能定理FL=1/2mv-1/2mv反映了力對空間的累積效應，是力在空間上的積分。
質點
內容：合外力做功等於物體動能的增量.
表達式： ΔW=ΔE
1.定理的使用對象是質點.
2.合外力的求法符合平行四邊形法則.
2‘.∑W=W+W+W+...+Wn
3.功是力在空間上的積累效果，也稱為力對位移的積分，這從功的定義式（如W=Fscosα）中可以看出，因此動能定理描述的是一段過程的變化。
4.動能沒有負值，但動能增量（末動能減初動能）可能為正，可能為負，也可能是零。
4‘.ΔE表示動能的增量。一般符號Δ都表示末狀態量減去初狀態量.
5.動能的增量為零，則合外力做功為零。但此時合外力不一定為零，各分力做功也不一定都為零，請特別注意.（舉例：水平面上的勻速圓周運動）
6.套用動能定理時，要注意參考系的一致。即所有物理量（如位移，速度）都取自同一參考系（參照物）。
7.參考系應選用慣性系。
8.動能定理刻畫了合外力的功與動能之間的變化關係。同樣的，其他性質的力和其相應能量之間的也有類似的恆等關係式，我們統稱其為功能關係。在動能定理的基礎上運用功能關係進行恆等變換，加以條件限制，便得出了一系列守恆定律，如機械能守恆定律等。條件限制對於這些守恆定律是很重要的，如機械能守恆定律的條件是除重力、彈力外沒有其他力做功。
9.動能定理、功能關係、能量守恆定律，雖然其表現形式和意義都不盡相同，但都是等價的。解決問題時，只需採用其中一個即可。
系統
由質點的動能定理，我們還可以得出更一般的系統的動能定理。
系統各組分合外力做功的代數和等於系統各組分動能增量的代數和
∑（∑W）=∑（△E）
在大多數情況下，系統各組分之間相互做的功其代數和都是零，此時套用系統的動能定理更為方便.但當系統各組分之間相互做功代數和不為零（如存在彈簧，相互引力、斥力等）的情況，應考慮內力做功，特別注意！
Fscosα代表作用在運動質點上的合外力的功（α代表力和水平方向的夾角）。應從動能定理深入領會“功”和“動能”兩個概念之間的區別和聯繫。動能是反映物體本身運動狀態的物理量。此定理體現了功和動能之間的聯繫。稱為定理的原因是因為它是從牛頓定律，經數學嚴格推導出來的，並不能擴大其套用範圍。由於動能定理不涉及物體運動過程中的加速度和時間，不論物體運動的路徑如何，因而在只涉及位置變化與速度的力學問題中，套用動能定理比直接運用牛頓第二定律要簡單。
推導過程
分析
（1）確定研究對象，研究對象可以是一個質點（單體）也可以是一個系統。
（2）分析研究對象的受力情況和運動情況，是否是求解“力、位移與速度關係”的問題。
（3）若是，根據動能定理ΔW=ΔE列式求解。
處理多過程問題
套用動能定理處理多過程運動問題關鍵在於分清整個過程有幾個力做功，及初末狀態的動能，採用動能定理處理問題無需考慮其具體的運動過程，只需注意初末狀態即可，求往復運動的總路程及次數問題，若用牛頓定律和運動學公式求解，必須用數列求和的方法，但對於其中的某些問題求解，如用動能定理求解，可省去不少複雜的數學推演，使解題過程簡化。
推導
對於勻加速直線運動有：
由牛頓第二運動定律得，
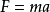動能定理①
勻加速直線運動規律有，
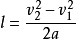動能定理②
①×②得，
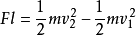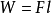動能定理
動能定理外力做功
，記
，
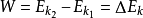動能定理即
對於非勻加速直線運動,
進行無限細分成n段，於是每段都可看成是勻加速直線運動（微元法思想）
對於每段運動有,
W=E-E
W=E-E
……
Wn=E-E將上式全部相加得
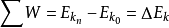動能定理推導完畢
解題步驟
分析
（1）確定研究對象，研究對象可以是一個質點（單體）也可以是一個系統。
（2）分析研究對象的受力情況和運動情況，是否是求解“力、位移與速度關係”的問題。
（3）若是，根據∑W=△Ek1列式求解。
推導
對於勻加速直線運動有：
由牛頓第二運動定律得
F=ma①
勻加速直線運動規律有：
s=((v2)^2-(v1)^2)/(2a)②
①×②得：
Fs=(1/2)m(v2)^2-(1/2)m(v1)^2
外力做功W=Fs，記Ek1=(1/2)m(v1)^2，Ek2=(1/2)m(v2)^2
即W=Ek2-Ek1=△Ek
對於非勻加速直線運動：
進行無限細分成n段，於是每段都可看成是勻加速直線運動（微分思想）
對於每段運動有：
W1=Ek1-Ek0
W2=Ek2-Ek1
……
Wn=Ekn-Ekn-1
將上式全部相加得
∑W=Ekn-Ek0=△Ek
推導完畢
