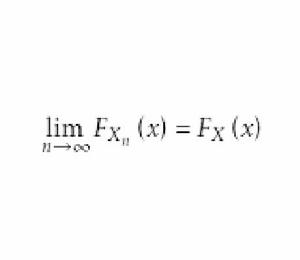定義
定義1
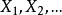 依分布收斂
依分布收斂 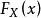 依分布收斂
依分布收斂 稱隨機變數序列 依分布收斂(convergence in distribution)於隨機變數X,如果對 的任意連續點x抄,都有
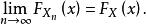 依分布收斂
依分布收斂 定義2
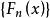 依分布收斂
依分布收斂 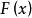 依分布收斂
依分布收斂 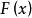 依分布收斂
依分布收斂 弱收斂 設 是一個分布函式列,如果存在一個分布函式 自,使得在 的每一個連續點上有
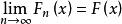 依分布收斂
依分布收斂 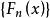 依分布收斂
依分布收斂 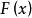 依分布收斂
依分布收斂 成立,則稱 弱收斂於 互,並記為
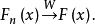 依分布收斂
依分布收斂 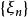 依分布收斂
依分布收斂 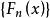 依分布收斂
依分布收斂 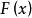 依分布收斂
依分布收斂 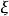 依分布收斂
依分布收斂 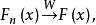 依分布收斂
依分布收斂 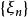 依分布收斂
依分布收斂 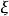 依分布收斂
依分布收斂 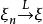 依分布收斂
依分布收斂 依分布收斂 設 為隨機變數序列, 是對應的分布函式列動,如果存在一個具有分布函式 的隨機變數 ,使得 則稱 依分布收斂於 ,並記作 。
我們必須指出,只有分布函式序列收斂到一個分布函式時,我們才說它是依分布收斂的,這一說明是必要的,因為分布函式序列可能收斂到一個函式,而這個函式不一定是一個分布函式。
實例分析
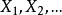 依分布收斂
依分布收斂 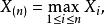 依分布收斂
依分布收斂 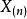 依分布收斂
依分布收斂 例1 (均勻樣本的最大值) 設 是獨立同分布的隨機變數,且都服從(0,1)區間上的均勻分布,令 問 是否依分布收斂、收斂於什麼?
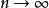 依分布收斂
依分布收斂 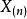 依分布收斂
依分布收斂 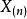 依分布收斂
依分布收斂 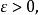 依分布收斂
依分布收斂 分析: 我們估計當 時 趨於1,事實上,由於 恆小於1,所以對任意 都有
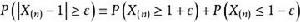 依分布收斂
依分布收斂 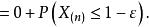 依分布收斂
依分布收斂 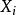 依分布收斂
依分布收斂 又因為 獨立同分布,所以
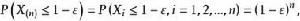 依分布收斂
依分布收斂 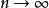 依分布收斂
依分布收斂 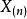 依分布收斂
依分布收斂 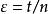 依分布收斂
依分布收斂 當 時趨於0,故 依機率收斂於1,然而,若令 ,則有
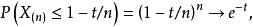 依分布收斂
依分布收斂 上式整理得
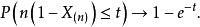 依分布收斂
依分布收斂 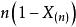 依分布收斂
依分布收斂 這就說明隨機變數 依分布收斂於某參數為1的指數型隨機變數。
注意,儘管我們定義的是隨機變數序列依分布收斂,其實質卻是累積分布函式而非隨機變數的收斂性,因此依分布收斂與依機率收斂、殆必收斂有著本質區別,不過,另兩種收斂都分別蘊含依分布收斂。
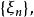 依分布收斂
依分布收斂 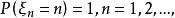 依分布收斂
依分布收斂 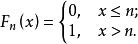 依分布收斂
依分布收斂 例2 考慮具有退化分布的隨機變數序列 若它的分布列為 這時 ,顯然,對任意的x∈R,有
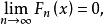 依分布收斂
依分布收斂 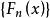 依分布收斂
依分布收斂 這表明序列 不收斂到一個分布函式。
相關定理
定理1
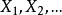 依分布收斂
依分布收斂 如果隨機變數序列 依機率收斂於隨機變數X,則該序列也依分布收斂於X。
定理2
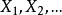 依分布收斂
依分布收斂 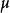 依分布收斂
依分布收斂 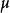 依分布收斂
依分布收斂 隨機變數序列 依機率收斂於常數 若且唯若該序列依分布收斂於 ,即,
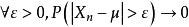 依分布收斂
依分布收斂 等價於
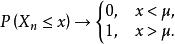 依分布收斂
依分布收斂