基本介紹
為更好地理解這種作圖方法,我們首先給出膨脹變換的定義 。
假設OA是已知圓⊙O(r)的半徑(圖1),今作一同心圓,使它的半徑恰好等於OA加上或減去(加與減指定其一)確定的一段AA',則所作的圓是一個確定的圓,像這般由已知圓⊙O(OA)變為一個確定的同心圓⊙O(OA')的變換,叫做 膨脹變換,其中線段AA'的長度a叫做 膨脹參數,在初等幾何學裡,一般都視圓的半徑和膨脹參數是正值,這樣一來,上述的膨脹變換便受到一定的局限性,以後為使膨脹變換普遍適用,我們約定(圖2):當a大於已知圓的半徑r時,⊙O(r)變為⊙O(|r- a|)的變換也看做是膨脹變換;特別地,當a = r即⊙O(|r-a|)成為點圓時,我們仍然一體看待。
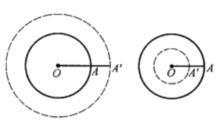 圖1
圖1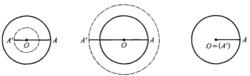 圖2
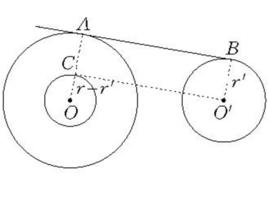
圖2若對相切兩圓⊙O(r)和⊙O'(r' )施行膨脹變換(圖3、4),使⊙O(r),⊙O'(r')分別變為⊙O(|r±a|)、⊙O'(|r'±a|),但其中雙號當原來兩圓外切時應一取正號一取負號 ,內切時同取正號或負號,那么所得兩圓仍然保持相切的性質,這個不變性對於相切圓的研究具有莫大的價值,因為它往往可以把某些問題化得簡單一些。
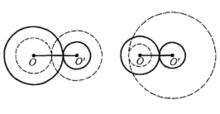 圖3
圖3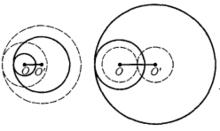 圖4
圖4除上述特性外,隨同膨脹變換的還有圓的切線隨著變換而進退,其進退的距離恰等於所選的膨脹參數,這些事理對作圖特別有用在中學課本上,關於兩圓公切線的作圖就是套用膨脹變換的原理而設計的。
套用膨脹變換的原理以解題,叫做 伸縮進退法。此法一般適用於有關圓和圓以及圓和直線相切的問題 。
例題解析
【例1】 求作一圓,使切於一個已知圓和兩條已知真線。
 圖5
圖5設定 ⊙P(R)和兩條直線a,b(圖5)。
求作 ⊙O,使切於⊙P和兩直線a,b。
分析 假設⊙O已作得,它的半徑為r。現在我們對⊙P(R)和⊙O(r)施行膨脹變換,使⊙P(R)變為點圓——點P,而⊙O(r)變為過P的一同心圓h,k的半徑等於R + r或|R-r|,視⊙P(R)與⊙O(r)外切或內切而定。在施行膨脹變換的同時, ⊙O(r)的切線a,b要隨著進退到離開原來位置等於R那樣遠的地方,臂如說,a進到a, b進到b。這樣一來,k實際就是通過已知點P且切於確定的兩直線a,b的圓,所以k有法求得,k既得,所求圓自然易於作出了。
作圖 作兩直線a,a同平行於a且令與a的距離都等於R;又作兩直線b,b同平行於b且令與b的距高都等於R。在所作的直線里,任選出兩條a,b(i,j = 1,2)來,然後作圓k使切於這兩條直線且通過點P。命k的圓心為O,若O與a,b有等距r,則⊙O(r)即是所求圓。
證明 據作圖,除已知⊙O(r)已和直線a,b相切外,又因k通辻點P且切於a,b兩直線,得知OP= R+r或|R-r|,可見⊙O(r)又與⊙P(R)相切,所以⊙O(r)合條件。
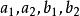 伸縮進退法作圖
伸縮進退法作圖推究 (1)假定a與b交於點E(圖5),那么將交成一個菱形ABCD,且直線AC,BD平分a與b的交角,因而E是該菱形的中心,由此可見,作出k後,必須圓心O落在射線EA,EB,EC,ED之一上面オ合用,從這處著眼,得知本題解數情形如下 :
①當⊙P不通過直線a與b的交點吋(圖6):
 圖6(a)
圖6(a)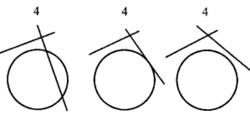 圖6(b)
圖6(b)a.如果⊙P與a,b都相交,則點P落在菱形ABCD內部,此時共得八解;
b.如果⊙P與a,b一交一切,則點P落在菱形ABCD某邊上,此時共得六解;
c.如果⊙P與a,b都相切,則點P是菱形ABCD的一個頂點,此時共得四解;
d.如果⊙P與a,b一交一離,則點P落在菱形ABCD某外角內,此時共得四解;
e.如果⊙P與a,b一切一離,則P點落在菱形ABCD某邊的延長線上,此時共得四解;
f.如果⊙P與a,b都相離,則點P落在菱形ABCD某角的對頂角內,此時共得四解。
②在⊙P通過直線a與b的交點時(圖7):
 圖7
圖7a.如果⊙P與a,b都相交,則點P落在菱形ABCD內部,但此時所作八個k中有四個合而為,並以點E為圓心,不合用,故僅得四解;
b.如果⊙P與a,b一交一切,則點P落在菱形ABCD某邊上,但此時所作六個k中有四個同上情形,不合用,故僅得兩解。
(2)假定a // b(圖8),則本題的解數情形如下:
①在⊙P與a, b都相交時四解;
②在⊙P與a,b一交一切時三解;
③在⊙P與a,b都相切時兩解;
④在⊙P與a,b一交離時兩解;
⑤在⊙P與a,b一切一離時:
a.當點P在a與b之間,三解;
b.當點P不在a與b之間,一解;
⑥在⊙P與a,b都相離時:
a.當點P在a與b之間,四解;
b.當點P不在a與b之間,無解 。
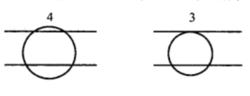 圖8(a)
圖8(a) 圖8(b)
圖8(b) 圖8(c)
圖8(c) 圖8(d)
圖8(d)