波形估計
正文
對於兩個相關的隨機過程y(t)和z(t),可以用第二個過程的某些觀測值z(ζ)來對第一個過程y(t)(一般稱為信號)的各種參量進行估計。如果用g(t)表示被估計的量，則g(t)可能是y(t)、懭(t)或y(t+α)等等。根據z(t)在時間軸上某一集合 I(從-∞到t中的一些離散點或一個區間）的觀測值，尋找一個合適的數據變換T，使它成為g(t)的最好估計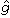
(t)。即 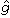(t)＝T【z(ζ),ζ∈I】
時，就是所謂預測問題。當
g(t)＝y(t)
時，就是所謂過濾問題。當g(t)＝y(t＋α)(α＜0,t∈【t0,tf】)
時，就是所謂平滑（或叫內插）問題。所謂最好的估計，是指這一估計所付出的“平均代價”最小。有各種不同的“代價”函式，如均方誤差代價(E｛(g(t)-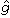(t))2｝)或平均絕對誤差代價(E｛│g(t)-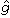(t)│｝)等 (E｛ ｝為求數學期望的符號)。如果z(t)是正態過程,對於均方誤差代價最好的估計T是線性的。對於非正態過程,則線性估計不一定最好。但是，由於線性估計比較簡單，所以常常被採用。對於平穩隨機過程，最好的線性波形估計就是著名的維納濾波。對於非平穩隨機過程，可以採用所謂卡爾曼濾波進行估計。