定理內容
引力真空場方程的球對稱解必靜態。
定理推導
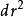 伯克霍夫定理
伯克霍夫定理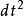 伯克霍夫定理
伯克霍夫定理靜態球對稱線元如果取消靜態條件線元表達式就會十分複雜,例如交叉項 非零,但可以通過適當的坐標變換把線元的形式變成和靜態的區別在於 和 前面的待定函式要從一元函式變為二元函式。通過不算太複雜的計算仍然得到史瓦西解。下面來作簡單證明。
這種情況下,可以證明其度規場總能化成
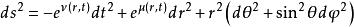 伯克霍夫定理
伯克霍夫定理其中兩個未知的函式
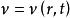 伯克霍夫定理
伯克霍夫定理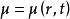 伯克霍夫定理
伯克霍夫定理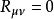 伯克霍夫定理
伯克霍夫定理應該要由真空場方程 解出.
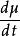 伯克霍夫定理
伯克霍夫定理這種情況下 和 不為零.因此克里斯多夫聯絡多出三個不為零的分量
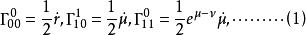 伯克霍夫定理
伯克霍夫定理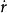 伯克霍夫定理
伯克霍夫定理 伯克霍夫定理
伯克霍夫定理 伯克霍夫定理
伯克霍夫定理 伯克霍夫定理
伯克霍夫定理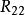 伯克霍夫定理
伯克霍夫定理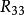 伯克霍夫定理
伯克霍夫定理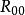 伯克霍夫定理
伯克霍夫定理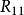 伯克霍夫定理
伯克霍夫定理其中 和 表示 和 對 的微商或者說導數,是牛頓的點記號.相應算出里契張量的分量 和 不變,但 和 添加了附加的項:
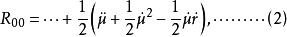 伯克霍夫定理
伯克霍夫定理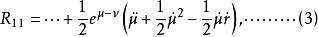 伯克霍夫定理
伯克霍夫定理 伯克霍夫定理
伯克霍夫定理這裡用的“ ”是代表原來的項.此外,里契張量多了一個非零分量
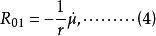 伯克霍夫定理
伯克霍夫定理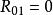 伯克霍夫定理
伯克霍夫定理又從場方程 導出
 伯克霍夫定理
伯克霍夫定理 伯克霍夫定理
伯克霍夫定理 伯克霍夫定理
伯克霍夫定理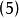 伯克霍夫定理
伯克霍夫定理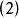 伯克霍夫定理
伯克霍夫定理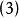 伯克霍夫定理
伯克霍夫定理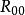 伯克霍夫定理
伯克霍夫定理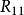 伯克霍夫定理
伯克霍夫定理它說明 仍然是 的函式. 時代回 和 式, 和 中的 附加項全部消失,從而場方程回復到
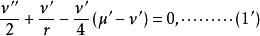 伯克霍夫定理
伯克霍夫定理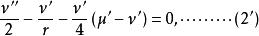 伯克霍夫定理
伯克霍夫定理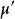 伯克霍夫定理
伯克霍夫定理 伯克霍夫定理
伯克霍夫定理其中, 和 分別表示其對 的微商或者說導數.
 伯克霍夫定理
伯克霍夫定理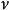 伯克霍夫定理
伯克霍夫定理上面的三個方程是 和 聯立的微分方程組,這三個方程只有兩個是獨立的,那是因為愛因斯坦張量必須滿足畢安基恆等式
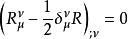 伯克霍夫定理
伯克霍夫定理的後果.
很容易解出
 伯克霍夫定理
伯克霍夫定理 伯克霍夫定理
伯克霍夫定理此時, 可以是 的 任意函式,
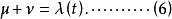 伯克霍夫定理
伯克霍夫定理再同樣算下去,得到的解是
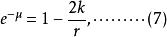 伯克霍夫定理
伯克霍夫定理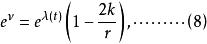 伯克霍夫定理
伯克霍夫定理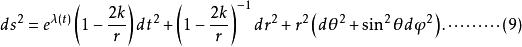 伯克霍夫定理
伯克霍夫定理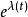 伯克霍夫定理
伯克霍夫定理這與史瓦西解的差別僅在第一個項多了一個.然而當我們對時間變數作如下變換
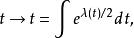 伯克霍夫定理
伯克霍夫定理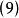 伯克霍夫定理
伯克霍夫定理之後,就回到了 史瓦西解,也就回到了定理內容所描述的 引力真空場方程的球對稱解必靜態。即伯克霍夫定理得證.
意義
定理的推導並不複雜,在相對論的基礎上所建立的許多成果都十分簡潔。伯克霍夫定理是個強有力的定理,他斷定非靜態物質分布只要保持球對稱性,即使是急劇收縮,膨脹,徑向震盪甚至爆炸,外部時空就仍由史瓦西度規來描述,這為研究星體演化提供了很大方便。
它的意義在於指明了史瓦西解描述的是一個 球對稱的外引力場,但是這個引力源 不用必須靜止.這就說明如果我們觀測的一個史瓦西引力場,我們便 無法判斷它的源是一個穩定的恆星,還是一個收縮的、膨脹的或者振盪的恆星。
作為定理的推廣,有如下結論: 一個球對稱質量分布在其中心的球形空腔中不產生引力場。這一結論在牛頓的引力理論中是顯然成立的:利用函式的唯一性定理可以證明,一個 均勻的球殼在其內部所產生的勢是常數。
定理的推導並不複雜,在相對論的基礎上所建立的許多理論都十分簡潔。

