定義
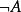 互補子
互補子 互補子
互補子如果A是一個原子公式,那么,A和互為對方的互補子,二者的關係稱為互補,互補關係以“”表示 。
相關概念
模型不包含互補對的基礎文字的一個集合稱為一個模型。令M是一個模型,S是一個基礎子句的集合,如果對於S中的所有元素C都包括M的元素,那么,M是S的模型。一般地,如果H是S中的Herbrand域,那么,僅當M是H(S)的模型。
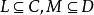 互補子
互補子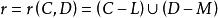 互補子
互補子基礎歸結原始表達式如果C和D是兩個基礎子句集,並且構成互補對集合,那么,基礎子句集稱為C和D的 基礎歸結原始表達式。
註:此定義是說,歸結的過程是在被賦值(半解釋)的子句中剔除(處於或關係中的)互補原子的過程。剔除互補原子後的子句集即基礎歸結原始表達式。
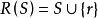 互補子
互補子基礎歸結 基礎子句集S的元素以及S的所有基礎歸結原始表達式構成的集合稱為 基礎歸結,以表示。
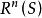 互補子
互補子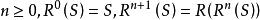 互補子
互補子n階基礎歸結如果S是一個基礎子句的集合,那么以表示S的 n階基礎歸結,它定義為:對於任何。
相關定理
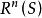 互補子
互補子 互補子
互補子定理1(Robinson第一定理)如果S是任意一個基礎子句的集合,那么,S是不可滿足的,若且唯若n≥0時,包含。
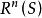 互補子
互補子 互補子
互補子充分性證明:如果包含,即包含至少一個互補對,在這種情況下,S不可能包含一個模型從由於S不包含一個模型M,因此S是不可滿足的。
 互補子
互補子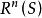 互補子
互補子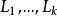 互補子
互補子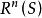 互補子
互補子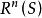 互補子
互補子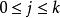 互補子
互補子 互補子
互補子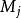 互補子
互補子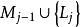 互補子
互補子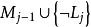 互補子
互補子 互補子
互補子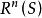 互補子
互補子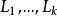 互補子
互補子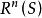 互補子
互補子 互補子
互補子必要性證明:只要證明,S如果不包含,那么就可以滿足。令是所有中的原子公式,或者它們的互補子在中。令M是一個模型,定義如下:對於,是空集,即集合,或。當從0逐步增大,這表示M將中的子句中的原子公式逐步擴展到M之中,即不包含,由於無矛盾的子句,即存在S為真的解釋,即S可滿足。
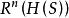 互補子
互補子 互補子
互補子定理2(Robinson第二定理)如果S是任意一個有窮子句的集合,那么,S是不可滿足的,若且唯若存在有窮個S的H化基例集H(S),包含。
證明:
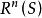 互補子
互補子 互補子
互補子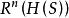 互補子
互補子 互補子
互補子根據Herbrand定理,S是不可滿足若且唯若存在有限的不可滿足的基例集H(S);根據Robinson第一定理,對於基礎子句集S,包含;而H(S)屬於基礎子句,所以包含。
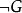 互補子
互補子綜上所述,給定一階命題G,在H上的基例集是H(S),則
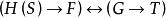 互補子
互補子是歸結方法。這是歸結證明方法的定義。
由此可見,歸結方法是一個綜合性的證明方法,這是因為它經過以下若干步驟,對於被證命題G:
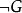 互補子
互補子求其否定命題:
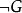 互補子
互補子求的Skolem標準型,消除量詞;
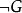 互補子
互補子求的子句集S;
求子句集S的D域;
求子句集S的H域;
求基例集H(S);
求原子集A;
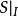 互補子
互補子求S的D解釋;
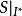 互補子
互補子求S的H解釋;
判定H(S)不可滿足性;
刪除子句文字中的互補句,驗證H(S)可滿足性。
這個過程是原理層面的揭示,不是操作層面的步驟。一般而言,在歸結操作層面,可不驗證H(S)的不可滿足性,而直接進行互補子句的消除,即進行子句的歸結,從而驗證子句的不可滿足性。
歸結方法雖然是通用的證明方法,但是它可以通過推理機實現(如Prolog),因此一般作為人工智慧的典型套用,即把它作為一種自動化的證明方法。但是,不通過自動證明也是可以完成的,因此它是一個獨立的證明方法,而不是機器證明的專有方法。
例題解析
例1n階基礎歸結。
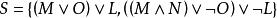 互補子
互補子給定子句集,有
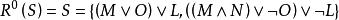 互補子
互補子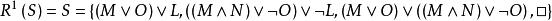 互補子
互補子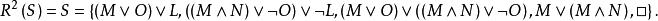 互補子
互補子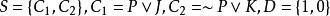 互補子
互補子例2設:,通過D賦值(半解釋):
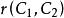 互補子
互補子(1)求基礎歸結原始表達式;
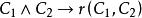 互補子
互補子(2)證明;
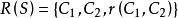 互補子
互補子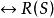 互補子
互補子(3)證明S與的不可滿足性是完全一致的(即S不可滿足不可滿足)。
解答:
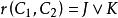 互補子
互補子(1)根據定義(基礎歸結),。
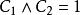 互補子
互補子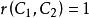 互補子
互補子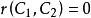 互補子
互補子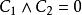 互補子
互補子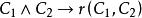 互補子
互補子(2)根據表1第3、4列,顯然有如果,則;如果,則,因此,成立。
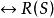 互補子
互補子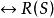 互補子
互補子(3)根據表1,第4列S和第5列R(S)的值完全一致,即S不可滿足不可滿足,S可滿足可滿足 。
| 1 | 2 | 3 | 4 | 5 | ||||||
| 賦值 | S的子句 | 基礎歸結原始表達式 | S(合取) | 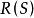 互補子 互補子 | ||||||
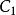 互補子 互補子 | 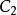 互補子 互補子 | 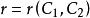 互補子 互補子 | 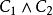 互補子 互補子 | 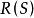 互補子 互補子 | ||||||
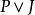 互補子 互補子 | 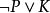 互補子 互補子 | 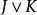 互補子 互補子 | 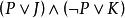 互補子 互補子 | 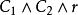 互補子 互補子 | ||||||
 互補子 互補子 | 1 | J | 1 | K | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | ||||
| 1 | 0 | K | 1 | 1 | 1 | 1 | 1 | 1 | ||
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | ||||
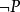 互補子 互補子 | 0 | J | 1 | K | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | ||||
| 0 | 0 | K | 1 | 0 | 1 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||

