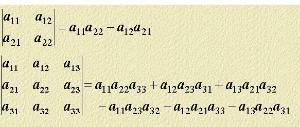基本內容
二項方程
二項方程 :
èr xiànɡ fānɡ chénɡ
形如axn b=0的方程,其中n為正整數,a、b≠0。將原方程化為xn=-ba的形式後,用複數開n次方的方法即可求解。它是用代數方法解一元n次方程的基礎。方程不用按逆向思維思考,可直接列出等式並含有未知數。它具有多種形式,如一元一次方程、二元一次方程等。廣泛套用於數學、物理等理科套用題的運算。
舉例
例1 解二項方程x-1=0
解 將等號左邊常數項-1移到等號右邊,可得x=1,
再根據複數開3次方的定義,可直接得出原方程的三個根為
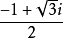 二項方程
二項方程x=1,x=
,x=
。
例2 解二項方程x-16=0
解法1 (直接開方法)將等號左邊常數項-1移到等號右邊,可得x=16,
再根據複數開4次方的定義,可直接得出原方程的四個根為
x=-2i,x=2i,x=-2,x=2。
解法2 (因式分解法)將等號左邊的二項式在R上因式分解,得(x+4)(x-4)=0,
再等號左邊的乘積在C上因式分解,得(x+2i)(x-2i)(x+2)(x-2)=0。
於是,要使原方程成立,等號左邊的四個因子至少有一個為0,
故x+2i=0,或x-2i=0,或x+2=0,或x-2=0。
這樣,就得到了原方程的四個根分別為x=-2i,x=2i,x=-2,x=2。
方程史話
1. 大約3600年前,古代埃及人寫在紙草上的數學問題中,就涉及了含有未知數的等式。
2. 公元825年左右,中亞細亞的數學家阿爾-花拉子米曾寫過一本名叫《對消與還原》的書,重點討論方程的解法。
2. 九章算術之一。
《後漢書·馬嚴傳》“善《九章筭術》” 唐 李賢註:“ 劉徽《九章算術》曰《方田》第一,《粟米》第二,《差分》第三,《少廣》第四,《商功》第五,《均輸》第六,《盈不足》第七,《方程》第八,《句股》(又作《勾股》)第九。”《九章算術·方程》 白尚恕注釋:“‘方’即方形,‘程’即表達相課的意思,或者是表達式。於某一問題中,如有含若干個相關的數據,將這些相關的數據並肩排列成方形,則稱為‘方程’。所謂‘方程’即現今的增廣矩陣。”
消元方法
代入消元法
例:解方程組x+y=5① 6x+13y=89②
解:由①得x=5-y③ 把③帶入②,得6(5-y)+13y=89,解得y=59/7
把y=59/7帶入③,得x=5-59/7,即x=-24/7
∴x=-24/7,y=59/7
這種解法就是代入消元法。
加減消元法
例:解方程組x+y=9① x-y=5②
解:①+②,得2x=14,即x=7
把x=7帶入①,得7+y=9,解得y=2
∴x=7,y=2
這種解法就是加減消元法。