概念
二次擴張(quadratic extension)是一類重要的有限擴張。二次擴張是指擴張次數為2的域擴張。域F上的二次不可約多項式的分裂域是F的二次擴張。設K/F是域擴張,K′是K的子域,F上的每個二次多項式在K′中可分解為一次因子的乘積,只要該多項式在K中有根,這樣的K′中的最小者,稱為F在K中的二次閉包。當F與它在代數閉包中的二次閉包一致時,稱F為二次閉域。
設A為交換環,e為A的單位元素。稱A的擴張B是二次擴張,如果存在B的元素v,使得(e,v)是A-模B的基。
設A為交換環,而d為A的元素。以關係:
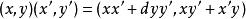 二次擴張
二次擴張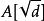 二次擴張
二次擴張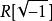 二次擴張
二次擴張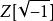 二次擴張
二次擴張定義乘法的加法群A 是A的二次擴張,在這一擴張中,(d,0)是(0,1)的平方;通常將這一擴張記為。例如,是複數體,是高斯整環。
擴張
如果E是一個域,而F是E的子集,它在E中加法和乘法的運算下也成 一個域,我們把E叫做F的一個擴張。E作為F的一個擴張時,可用符號F⊂E表示。如果F⊂E, 且不考慮E的元素間所定義的乘法運算,那么可把E當作是F上的一個向量空間。如果F上向量空間E的維數(記作E/F)是有限的,那么把E叫做有限擴張。
域的擴張
域論的基本概念之一。若域K包含域F作為它的子域,則稱K是F的一個擴張(或擴域),F稱為基域,常記為K/F。此時,K可以看成F上的向量空間。研究擴域K(相對於基域F)的代數性質,是域論研究的一個基本內容。
若域E是F的擴域,K是E的擴域,則稱E是域擴張K/F的中間域。若K/F是域擴張,S是K的子集,且F(S)是K的含F與S的最小子域,稱F(S)為F添加S的擴域。當S={α,α,…,α}是有限集合時,F(α,α,…,α)稱為添加α,α,…,α於F的有限生成擴域(或者F上的有限生成擴張)。它由一切形如:f(α,α,…,α)/g(α,α,…,α)的元組成,其中α,α,…,α∈S,f,g是F上的n元多項式且g(α,α,…,α)≠0。
由於這個原因,當F(α,α,…,α)關於F的超越次數≥1時,F(α,α,…,α)也稱為F上的代數函式域。當S={α}時,稱F(α)為F的單擴張域,也稱本原擴域。F的有限代數擴域K是單擴域的充分必要條件是,擴域K與基域間存在有限箇中間域。這是施泰尼茨(Steinitz,E.)證明的。
閉包
圖論的一個基本概念。指由一個圖所派生出的另一個圖.具體地說,一個圖G的閉包H是指符合下列條件包含邊最少的圖:G是H的支撐子圖;對於H上任何兩不相鄰節點v和w,都有ρ(v)+ρ(w)<n,這裡n表示H的階,ρ(v)和ρ(w)分別表示圖H上節點v和w的次。所謂閉包運算,就是如下從圖G得到它的閉包的遞歸過程:連通圖G上任何一對不相鄰且滿足ρ(u)+ρ(v)≥n的節點u和v連一邊,這裡ρ(u)和ρ(v)分別表示u,v在G上的次,而n表示G的階;對所得的圖仍進行這種運算,直到得到這樣的圖H,對於任何一對不相鄰節點u和v均有ρ(u)+ρ(v)<n成立。奧爾(Ore,O.)於1961年證明:若一個連通的簡單圖G,對於任何兩個不相鄰的節點,它們的次之和不小於G的階,則G必為哈密頓圖。稱節點次之和特別是兩個節點次之和所滿足的條件為奧爾型條件。所謂一個圖G的k閉包,是指符合下列條件且包含邊最少的圖H:G是H的支撐子圖;對於H上任何兩不相鄰節點v和u,都有ρ(v)+ρ(u)<k,0<k≤2n-4。於是,n階圖的閉包就是n閉包。這種與閉包運算類似的求一個圖的k閉包的過程稱為k閉包運算。設P是n階圖上的某種性質。在一個n階圖G上的兩個不相鄰的節點u,v,它們次之和ρ(u)+ρ(v)≥k。若G+(u,v)(即在G上加一條新邊所得的圖)具有性質P可以導出G本身也具有性質P,則稱P是k穩定的。若P是k穩定,則從一個圖的k閉包具有性質P可以導出它本身也有性質P。具有哈密頓圈的性質是n穩定的。
代數閉包
一個域的最大代數擴域。若域F的代數擴域Ω為代數閉域,則稱Ω為域F的一個代數閉包。一個域F的代數閉包總是存在的,並且在F同構意義下惟一。這個基本定理來自施泰尼茨(Steinitz,E.)。設K是域F的擴域,在K中F上代數元的全體組成的子域A稱為F在K內的代數閉包,它是F在K內的最大代數擴域。特別地,若F=A,則稱F在K內是代數閉的。
實線性空間中的集合的代數意義下的閉包。設A為實線性空間X中的集合。A的代數閉包是指這樣的點b∈X的全體:存在h∈X,對於任何ε>0,存在λ∈[0,ε],使得b+λh∈A.A的代數閉包常記為acl(A)。如果A=acl(A),那么A稱為代數閉集。它也是X在以代數開集為開集的拓撲意義下的閉集,即代數閉集的余集必定是代數開集;反之亦然。代數閉包的概念在敘述凸集分離定理時也起重要作用。
有的文獻定義代數閉包時,要求對於任何λ∈(0,ε)都有b+λh∈A.這時代數閉集就不再是代數開集的余集。但當A是多於一點的凸集時,由這兩種定義得到的代數閉包是相同的。
