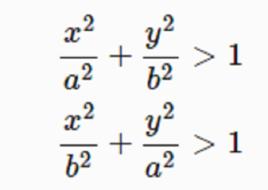定義
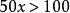 二次不等式
二次不等式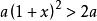 二次不等式
二次不等式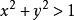 二次不等式
二次不等式當不等式兩端是含有n個(n是自然數)未知數的整式時,則根據整式的次數分別叫做n元一次不等式,n元二次不等式等等。例如,不等式 是一元一次不等式, 是一元二次不等式;而不等式 則是二元二次不等式。 二次不等式(quadratic inequality)是一種整式不等式,如果整式不等式的次數是2,則稱為二次不等式,若二次不等式有n個未知數,則稱為n元二次不等式。
一元二次不等式
定義:含有一個未知數,且的未知數的最高次數是二次的不等式叫作一元二次不等式。
一元二次不等式的解法:
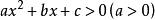 二次不等式
二次不等式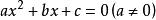 二次不等式
二次不等式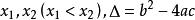 二次不等式
二次不等式(1)一元二次不等式,設相應的一元二次方程的兩根為。
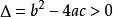 二次不等式
二次不等式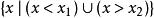 二次不等式
二次不等式若,一元二次不等式的解集為;
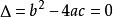 二次不等式
二次不等式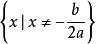 二次不等式
二次不等式若,一元二次不等式的解集為;
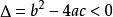 二次不等式
二次不等式若,解集為 R。
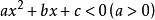 二次不等式
二次不等式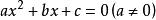 二次不等式
二次不等式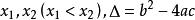 二次不等式
二次不等式(2)一元二次不等式,設相應的一元二次方程的兩根為。
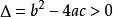 二次不等式
二次不等式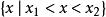 二次不等式
二次不等式若,一元二次不等式的解集為;
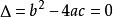 二次不等式
二次不等式 二次不等式
二次不等式若,一元二次不等式的解集為;
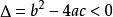 二次不等式
二次不等式 二次不等式
二次不等式若,一元二次不等式的解集為。
二元二次不等式
定義1 一個二元二次方程表示一條圓錐曲線,為簡便計,這裡只研究具有標準形式(非退化)的圓錐曲線方程所對應的不等式表示的區域。
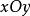 二次不等式
二次不等式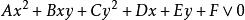 二次不等式
二次不等式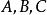 二次不等式
二次不等式定義2 平面上所有滿足二元二次不等式(不全為零)的點的集合,叫作這個二元二次不等式表示的區域,這裡“V”表示“>”,“<”,“≥”,“≤”四種中的一種。
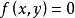 二次不等式
二次不等式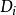 二次不等式
二次不等式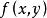 二次不等式
二次不等式定理1 在曲線所劃分的每個平面開區域內,多項式或者永遠是正的,或者永遠是負的。
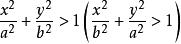 二次不等式
二次不等式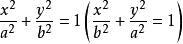 二次不等式
二次不等式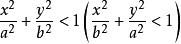 二次不等式
二次不等式定理2 不等式表示橢圓的外部的開區域;不等式表示橢圓的內部的開區域(圖1,圖2)。
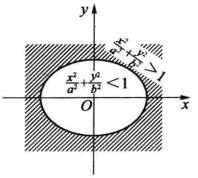 圖1
圖1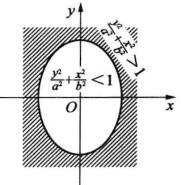 圖2
圖2定義3 設圓錐曲線方程c:
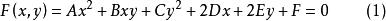 二次不等式
二次不等式稱含有焦點的區域為圓錐曲線的 內域,不含焦點的區域為圓錐曲線的 外域 (證明過程請參考相應參考資料)。
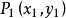 二次不等式
二次不等式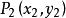 二次不等式
二次不等式定理3 點和在(1)的同一區域(或不同區域)的充要條件是
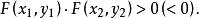 二次不等式
二次不等式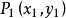 二次不等式
二次不等式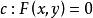 二次不等式
二次不等式定理4 點在圓錐曲線的內域(或外域)的充要條件是
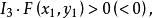 二次不等式
二次不等式其中
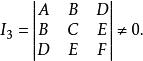 二次不等式
二次不等式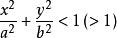 二次不等式
二次不等式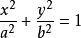 二次不等式
二次不等式推論: 的解域是橢圓的內域(或外域);
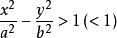 二次不等式
二次不等式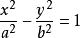 二次不等式
二次不等式的解域是雙曲線的內域(或外域);
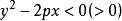 二次不等式
二次不等式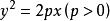 二次不等式
二次不等式的解域是拋物線的內域(或外域)。