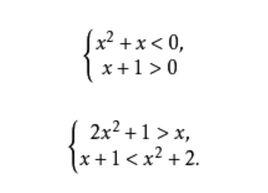基本概念
一元二次不等式組是一種常見的不等式組，指在含有同一個未知數的整式不等式組中，至少有一個是二次的不等式組，例如
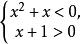一元二次不等式組與
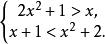一元二次不等式組一元二次不等式組的求解步驟
不等式組中各不等式的解集的交集是不等式組的解集。
其求解的一般步驟是：
1.解不等式組中的各不等式（見“一元二次不等式”）。
2.取各不等式解集的交集，即得一元二次不等式組的解集。可以將各不等式的解在同一數軸上表示出來，它們的公共部分就是不等式組的解集 。
例題解析
一元二次不等式組的解法，與一元一次不等式組的解法一樣。先解出這個不等式組中的每一個不等式，再找出它們解的公共部分，就得到原不等式組的解 。
【例1】解不等式組:
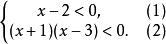一元二次不等式組解 不等式(1)的解是x<2，不等式(2)的解是﹣1<x<3，它們的公共部分是﹣1<x<2。
所以原不等式組的解是﹣1<x<2。 在數軸上表示，如圖1所示。
圖1【例2】解不等式組：
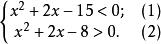一元二次不等式組解 不等式(1)就是(x+5)(x－3)<0，它的解為﹣5<x<3；而不等式(2)就是(x+4)(x－2)>0， 它的解為x<﹣4或x>2。
這兩個不等式的公共部分是﹣5<x<﹣4或2<x<3，所以原不等式組的解是﹣5<x<﹣4或2<x<3，在數軸上表示，如圖2所示 。
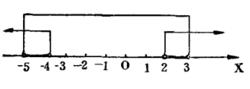圖2