原理
計算步驟
 二分搜尋算法
二分搜尋算法 二分搜尋算法
二分搜尋算法 二分搜尋算法
二分搜尋算法 二分搜尋算法
二分搜尋算法 二分搜尋算法
二分搜尋算法 二分搜尋算法
二分搜尋算法 二分搜尋算法
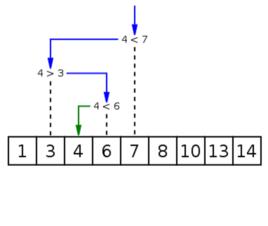
二分搜尋算法給予一個包含 個帶值元素的數組 或是記錄,使 ,以及目標值 ,還有下列用來搜尋 在 中位置的子程式。
 二分搜尋算法
二分搜尋算法 二分搜尋算法
二分搜尋算法 二分搜尋算法
二分搜尋算法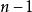 二分搜尋算法
二分搜尋算法令 為 , 為 。
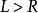 二分搜尋算法
二分搜尋算法如果 ,則搜尋以失敗告終。
 二分搜尋算法
二分搜尋算法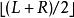 二分搜尋算法
二分搜尋算法令 (中間值元素)為 。
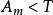 二分搜尋算法
二分搜尋算法 二分搜尋算法
二分搜尋算法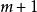 二分搜尋算法
二分搜尋算法如果 ,令 為 並回到步驟二。
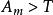 二分搜尋算法
二分搜尋算法 二分搜尋算法
二分搜尋算法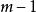 二分搜尋算法
二分搜尋算法如果 ,令 為 並回到步驟二。
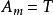 二分搜尋算法
二分搜尋算法 二分搜尋算法
二分搜尋算法當 ,搜尋結束;回傳值 。
這個疊代步驟會持續通過兩個變數追蹤搜尋的邊界。有些實際套用會在算法的最後放入相等比較,讓比較循環更快,但平均而言會多一層疊代。
大致匹配
以上程式只適用於 完全匹配,也就是查找一個目標值的位置。不過,因為有序數組的順序性,將二分搜尋算法擴展到能適用大致匹配並不是很重要。舉例來說,二分搜尋算法可以用來計算一個賦值的 排名(或稱 秩,比它更小的元素的數量)、 前趨(下一個最小元素)、 後繼(下一個最大元素)以及 最近鄰。搜尋兩個值之間的元素數目的範圍查詢可以藉由兩個排名查詢(又稱 秩查詢)來運行。
•排名查詢可以使用調整版的二分搜尋來運行。藉由在成功的搜尋回傳{\displaystyle m},以及在失敗的搜尋回傳{\displaystyle L},就會取而代之地回傳了比起目標值小的元素數目。
•前趨和後繼查詢可以藉由排名查詢來運行。一旦知道目標值的排名,其前趨就會是那個位於其排名位置的元素,或者排名位置的上一個元素(因為它是小於目標值的最大元素)。其後繼是(數組中的)下一個元素,或是(非數組中的)前趨的下一個元素。目標值的最近鄰可能是前趨或後繼,取決於何者較為接近。
•範圍查詢也是直接了當的。一旦知道兩個值的排名,不小於第一個值且小於第二個值的元素數量就會是兩者排名的差。這個值可以根據範圍的端點是否算在範圍內,或是數組是否包含其端點的對應鍵來增加或減少1。
複雜度分析
時間複雜度
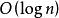 二分搜尋算法
二分搜尋算法折半搜尋每次把搜尋區域減少一半,時間複雜度為 。(n代表集合中元素的個數)
空間複雜度
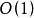 二分搜尋算法
二分搜尋算法,雖以遞歸形式定義,但是尾遞歸,可改寫為循環。