簡介
二元周期序列是一種特殊的序列，即只取兩個非0數值的周期序列。
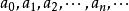二元周期序列
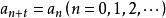二元周期序列 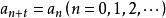二元周期序列
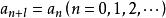二元周期序列設序列為 ，若存在正整數t，使 成立，則稱序列為二元周期序列，並稱滿足 式的最小正整數t為序列的周期。如果有正整數l，使 ，則t|l。
自相關值
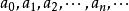二元周期序列
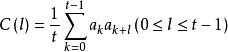二元周期序列 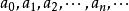二元周期序列
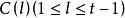二元周期序列 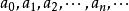二元周期序列設序列 的周期為t，記 ，則稱C(0)=1為序列 的自相關主值，稱 為序列 的自相關非主值。
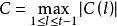二元周期序列 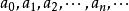二元周期序列若定義 ，如果C很小，則稱序列是自相關良好的序列。取值為±1的自相關良好的周期序列，在數字通信中有重要套用。
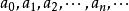二元周期序列
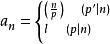二元周期序列設p為奇素數，且定義序列中的，則有C≤3/p。按照定義的序列稱為二次剩餘序列。當p較大時，它也是一個自相關良好的序列。
套用
一個二元周期序列若滿足以下三個條件：
1、周期很長；
2、一個周期中0和1的個數大約各占一半，並且它們在周期中的分布不能集中，而是看上去像是隨機的。確切的說，就是在一個周期中相鄰兩數字00，01，10和11出現的頻率也比較平均，八個相鄰三位數字000，001，010，011，100，101，110，111在一個周期中出現的也比較平均；
3、自相關性能好。
則我們稱這個二元周期序列偽隨機性好。
統計分析理論表明：序列的自相關非主值愈小，表明周期中各位數字彼此不相關。不僅是相鄰數字之間，而且不相鄰的數字也關係不明顯。所以，自相關良好的序列不僅用到通信同步問題上，也是保密的密鑰序列所需要的。
