擴頻碼序列是指擴頻碼的二進制序列,它是很窄的脈衝碼序列,其碼速率是很高的。
在擴頻通信中常需要用高碼速率的窄脈衝序列,這是針對擴頻碼序列的波形而言,並未涉及碼的結構和如何產生等問題,現在實際中用的最多的是偽隨機碼,或稱為PN碼。這類碼序列最重要的特性是具有近似於隨機信號的性能。因為噪聲具有完全的隨機性,也就是說具有近似於噪聲的性能。但是,真正的隨機信號和噪聲是不能重複再現和產生的,只能產生一種周期性的脈衝信號來近似隨機噪聲的性能,故稱為隨機碼。
基本特性
一般來說,理想的擴頻碼序列應具有如下特性:
(1)有尖銳的自相關特性;
(2)儘可能小的互相關值;
(3)足夠多的序列數;
(4)有儘可能大的序列複雜度;
(5)序列平衡;
(6)工程上易於實現。
偽隨機序列
在擴頻通信中通常需要高碼速的窄脈衝序列作為擴頻碼,實際上用的最多的是偽隨機碼序列,或稱為偽噪聲(PN)碼序列。這類碼序列最重要的特性是具有近似於隨機信號的性能。按照香農資訊理論,在高斯白噪聲信道上,最佳的信號是具有白噪聲統計特性的信號,其原因是高斯白噪聲具有最大的隨機性。但是,真正的隨機信號和噪聲是不能重複再現和產生的。我們只能產生一種周期性的脈衝信號來近似隨機噪聲的性能,故稱為偽隨機碼或PN碼。
對偽隨機碼最基本的要求是具有隨機性。這種隨機性可以用自相關函式來衡量。自相關函式可以表示信號與其自身相移以後的相似性。
特點
在工程上常用二元{0,1}序列組成偽噪聲(PN)碼。它具有如下特點:
(1)每一周期內,0和1出現的次數近似相等;
(2)每一周期內,長度為n比特的遊程出現的次數比長度為n+1比特遊程次數多一倍;
(3)序列具有雙值系相關函式;
偽隨機信號
擴頻技術是選用具有上述偽隨機特性的碼序列與待傳信息流波形相乘或序列模2加之後的複合信號,對射頻載波進行調製,然後送入信道進行傳輸。因此,作為擴頻函式的偽隨機信號,應具有以下特點:
(1)偽隨機信號必須具有尖銳的自相關函式,而互相關函式應接近於零;
(2)有足夠長的碼周期,以確保抗偵破、抗干擾的要求;
(3)有足夠多的獨立地址數,以便滿足碼分多址的要求;
(4)工程上易於產生、加工、複製和控制。
常用的偽隨機序列
擴頻碼序列是偽隨機序列,最簡單的、最常見的、使用最多的是m碼序列或Gold碼序列。
1.m序列。
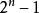 擴頻碼序列
擴頻碼序列m序列是在一定級數的位移暫存器情況下,所能產生周期最長的PN碼。由於m序列容易產生,規律性強,有許多優良的性能,所以在擴頻通信中最早獲得廣泛的套用。m序列是由多位級移暫存器或其它延遲元件通過線性反饋產生的最長的碼序列。在二進制位移暫存器發生器中,若n為級數,則能產生的最大長度的碼序列為 位。m序列的最大長度決定於位移暫存器的級數,而碼的結構決定於反饋抽頭的位置和數量。不同的抽頭組合可以產生不同長度和不同結構的碼序列。有的抽頭組合併不能產生最長周期的序列。對於何種抽頭能產生何種長度和結構的碼序列,已經進行了大量的研究工作。現在已經得到3~100級m序列發生器的連線圖和所產生的的m序列的結構。
m序列有如下性質:
(1)在m序列中的一個周期內“1”的數目比“0”的數目多1位。
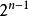 擴頻碼序列
擴頻碼序列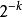 擴頻碼序列
擴頻碼序列(2)在一個序列中連續出現的相同碼稱為一個遊程,連碼的個數稱為遊程的長度。m序列中共有 個遊程,其中長度為1的遊程占遊程總數的1/2,長度為2的遊程占遊程總數的1/4,長度為3的遊程占遊程總數的1/8,依次類推,長度為k的遊程占 。其中最長的遊程是n個連1碼,次長的遊程是n-1個連0碼。
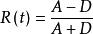 擴頻碼序列
擴頻碼序列(3)m序列的自相關函式由下式計算: ,其中A為0的位數,D為1的位數。
(4)m序列和其移位後的序列逐位模2相加,所得的序列還是m序列,只是相移不同而已。
(5)m序列發生器中移位暫存器的各種狀態,除全0狀態外,其他狀態只在m序列中出現一次。
(6)m序列發生器中,並不是任何抽頭組合都能產生m序列。
在上述m序列的前三個性質正是其隨機性的表現。後三個性質在實際套用中都很有用。
2.Gold碼序列。
Gold序列是1967年R.Gold在m序列基礎上提出並分析的一種特性較好的偽隨機序列,它是由兩個碼長相等、碼時鐘速率相同的m序列優選對通過模2相加而構成的。
通過設定m序列發生器B的不同初始狀態,可以得到不同的Gold序列,由於總共有m-1個不同的相對移位(Q為m序列的級數),加上原有的兩個m序列,可以產生共m+1個Gold序列。
Gold碼序列是一種基於m序列的碼序列,具有較優良的自相關和互相關特性,產生的序列數多。Gold碼的自相關性不如m序列,具有三值自相關特性;互相關性比m序列要好,但還沒有達到最佳。
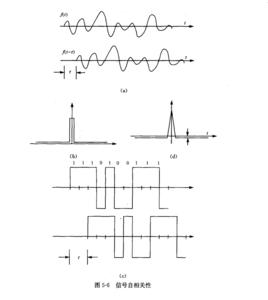
相關性
選用隨機信號或具有噪聲性能的信號來傳輸信息是因為許多理論研究表明,在信號傳輸中各種信號之間的差別性能越大越好。這樣任意兩個信號不容易混淆,也就是說,相互之間不容易發生干擾,不會發生誤判。理想的傳輸信號的信號形式應是類似於噪聲的隨機信號,因為取任何時間上不同的兩段噪聲比較都不會完全相似。它們代表兩種信號,其差別性就會最大。
在數學上是用自相關函式來表示信號和它自身相移以後的相似性的。隨機信號的自相關函式可定義為:
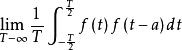 擴頻碼序列
擴頻碼序列φ=
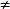 擴頻碼序列
擴頻碼序列 擴頻碼序列
擴頻碼序列若a 0,則φ=0;若a=0,則φ=常數。式中。 為信號的時間函式,a為時間延遲。
 擴頻碼序列
擴頻碼序列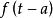 擴頻碼序列
擴頻碼序列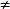 擴頻碼序列
擴頻碼序列上式的物理概念是 與其相對延遲的a的 來比較:如二者不完全重疊,即a 0,則乘積的積分為0;若兩者完全重疊,即a=0,則乘積的積分為一常數。
 擴頻碼序列
擴頻碼序列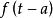 擴頻碼序列
擴頻碼序列因此上式中值得大小可用來表征 與自身延遲後的 的相關性,故稱為自相關函式。