概述
89C5l系列單片機歷經20多年的發展，仍然長盛不衰，在工業控制及儀器儀表中得到廣泛套用；用於89C5l單片機軟體開發的KeilC51編譯系統也日臻成熟，成為89C5l系列單片機軟體開發的優先選擇。在單片機系統開發中，經常遇到整數二十進制轉換的問題，一般可以採用C語言中的標準函式sprintf()來實現；但由於該函式是通用格式輸出函式，代碼量大(超過lKB)，用於整數二一十進制轉換的運算時間過妊(在12MHz晶振頻率下超過lms)，這在計算密集(computationintensive)的套用中是一個影響系統性能的重要因素。在低功耗系統設計中，也必須考慮因為運算時間長而增加系統耗電量的問題。經常有網發詢問如何高效地實現這種轉換。筆者通過對二進制整數的深入分析，巧妙運用89C5l單片機的特殊單位元組乘除指令，成功地實現了整數二一十進制轉換的快速算法。本文將詳細介紹快速算法，給出頗具實用性的最佳化代碼，並與使用sprintf()函式的實現及傳統的彙編代碼實現進行性能比較。
算法
要實現快速運算，很自然地想到教科書中提到的雙位元組二進制整數轉換成3位元組BCD碼整數的子程式。其採用的算法是，依次將整數的每位左移至CY位，再把CY位左移至一個3位元組佇列中，並進行十進制調整。通過16次移位完成運算，結果為壓縮格式的3位元組BCD編碼。
彙編子程式如下：
二一十進制編碼快速算法
快速算法從千位入手，首先求取整數中包含l000的個數(以下稱為“千數”)。求取了千數，其他問題就迎刃而解了。
設二進制整數以b=[b15…b0]表示，取值範圍為O～65535。其高6位[b15…b10]取值範圍為0～63，在整數中代表的數值為(0～63)*1024；後10位[b9…b0]代表的數值範圍為O～l023。可以寫出如下算式：
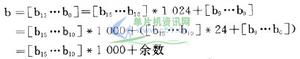二一十進制編碼可以用[b15…b10]作為整數中千數的預估。
餘數的最大值為63×24+1023=2535。這表明餘數中最多還有2個l000，也就是說千數的預估誤差最多為2，因此最多通過2次校正，就可求得千數的準確值。2次校正方法：
①如果餘數高位位元組≥4(即餘數≥1024，這樣用只是為了簡化代碼；也可以用餘數≥1000的判定條件)，則千數+l，餘數～1000；
②如果餘數≥l000，則千數+1，餘數～l000。
至此就求出了千數。千數用10整除所得商和模余作為萬位數和千位數。
從餘數中求取百、十，個位數也很簡單：
餘數用100整除得到百位數。實際是先把餘數右移2位，此時已成單位元組數，再用單位元組除指令進行除以25的操作，即得到百位數；而除去百位後的餘數已是單位元組數，可輕易取得十位數與個位數。
用C語言編寫的函式如下：
二一十進制編碼