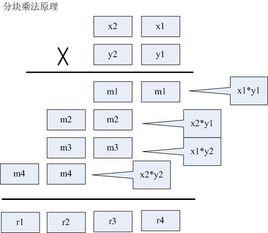
統計學描述
若某個對象分為n個環節,第1個環節有m個元素,第2個環節有m個元素,……,第n個環節有m個元素,則該對象有 N=m×m×m×…×m 種序列。
數學描述
例1、求取矩形的面積。
對於矩形,長、寬可以看做分別在二維空間的兩個維內,且兩個維相互正交,如果缺少長、寬中任何一個,矩形面積就失去意義,則矩形面積與長、寬的關係為:面積=長x寬。
例2、求取矩形的周長。
對於矩形的周長,長、寬雖然在二維空間的兩個維內,且兩個維相互正交,但是如果缺少長、寬中任何一個,周長仍然有意義(還是長度,只是不完整),則周長與長、寬的關係為:周長=長+寬+長+寬。
例3、現有4筐蘋果,每筐20千克,求總共蘋果(W)有多少千克?
證明
 乘法原理
乘法原理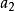 乘法原理
乘法原理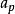 乘法原理
乘法原理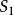 乘法原理
乘法原理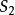 乘法原理
乘法原理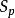 乘法原理
乘法原理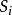 乘法原理
乘法原理 乘法原理
乘法原理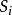 乘法原理
乘法原理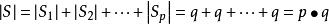 乘法原理
乘法原理乘法原理是加法原理的一個推論,令 , ,…, 是對元素a的p個不同的選擇。將S劃分成部分 , ,…, ,其中 是S內第一個元素為 (i=1,2,…,p)的有序偶的集合。每個 的大小為q,因此由加法有
上述推導用到了整數的乘法就是重複的加法這一事實。
例題
例如,從A城到B城中間必須經過C城,從A城到C城共有3條路線(設為a,b,c),從C城到B城共有2條路線(設為m,t),那么,從A城到B城共有3×2=6條路線,它們是:
 乘法原理
乘法原理am,at,bm,bt,cm,ct.
下面我們通過一些例子來說明這兩個原理在計數中的套用.
例1
利用數字1,2,3,4,5共可組成
⑴多少個數字不重複的三位數?
⑵多少個數字不重複的三位偶數?
⑶多少個數字不重複的偶數?
解:⑴百位數有5種選擇;十位數有4種選擇;個位數有3種選擇.所以共有
5×4×3=60
個數字不重複的三位數.
⑵ 先選個位數,共有兩種選擇:2或4.在個位數選定後,十位數還有4種選擇;百位數有3種選擇.所以共有
2×4×3=24
個數字不重複的三位偶數.
⑶ 分為5種情況:
一位偶數,只有兩個:2和4.
二位偶數,共有8個:12,32,42,52,14,24,34,54.
三位偶數由上述⑵中求得為24個.
四位偶數共有2×(4×3×2)=48個.括弧外面的2表示個位數有2種選擇(2或4).
五位偶數共有2×(4×3×2×1)=48個.
由加法原理,偶數的個數共有
2+8+24+48+48=130.
例2
從1到300的自然數中,完全不含有數字3的有多少個?
解法1: 將符合要求的自然數分為以下三類:
⑴一位數,有1,2,4,5,6,7,8,9共8個.
⑵二位數,在十位上出現的數字有1,2,4,5,6,7,8,9 8種情形,在個位上出現的數字除以上八個數字外還有0,共9種情形,故二位數有8×9=72個.
⑶三位數,在百位上出現的數字有1,2兩種情形,在十位、個位上出現的數字則有0,1,2,4,5,6,7,8,9九種情形,故三位數有
2×9×9=162個.
因此,從1到300的自然數中完全不含數字3的共有
8+72+162=242個.
解法2: 將0到299的整數都看成三位數,其中數字3
不出現的,百位數字可以是0,1或2三種情況.十位數字與個位數字均有九種,因此除去0共有
3×9×9-1=242(個).
例3
在小於10000的自然數中,含有數字1的數有多少個?
解: 不妨將1至9999的自然數均看作四位數,凡位數不到四位的自然數在前面補0.使之成為四位數.
先求不含數字1的這樣的四位數共有幾個,即有0,2,3,4,5,6,7,8,9這九個數字所組成的四位數的個數.由於每一位都可有9種寫法,所以,根據乘法原理,由這九個數字組成的四位數個數為9×9×9×9=6561,
所以比10000小的不含數字1的自然數的個數是6561+1=6562(算上0),於是,小於10000且含有數字1的自然數共有10000-6562=3438個.
例4
求正整數1400的正因數的個數.
解: 因為任何一個正整數的任何一個正因數(除1外)都是這個數的一些質因數的積,因此,我們先把1400分解成質因數的連乘積
1400=2×2×2×5×5×7
所以這個數的任何一個正因數都是由2,5,7中的n個相乘而得到(有的可重複).於是取1400的一個正因數,這件事情是分如下三個步驟完成的:
⑴ 取2×2×2的正因數是1,2,2×2,2×2×2,共3+1種;『註:1表示取0個;2表示取1個2;2×2表示取2個2;2×2×2表示取3個2.下面同理』
⑵ 取5×5的正因數是1,5,5×5,共2+1種;
⑶ 取7的正因數是1,7,共1+1種.
所以1400的正因數個數為
(3+1)×(2+1)×(1+1)=24.
說明: 利用本題的方法,可得如下結論:
若將正整數a分解成質因數pi(i=1,2,…,r)的連乘積時,其中質因數pi的個數是ai(i=1,2,…,r),則正整數a的不同的正因數的個數是
(a1+1)×(a2+1)×…×(ar+1).
例5
求五位數中至少出現一個6,且能被3整除的數的個數.
解答如下:
⑴ 從左向右計,如果最後一個6出現在第5位,即a5=6,那么a2,a3,a4可以是0,1,2,3,4,5,6,7,8,9這十個數字之一,但a1不能是任意的,它是由a2+a3+a4+a5被3除後的餘數所決定.因此,為了保證a1+a2+a3+a4+a5能被3整除,a1隻有3種可能,根據乘法原理,5位數中最後一位是6,而被3整除的數有
3×10×10×10=3000(個).
⑵ 最後一個6出現在第四位,即a4=6,於是a5隻有9種可能(因為a5不能等於6),a2,a3各有10種可能,為了保證a1+a2+a3+a4+a5被3整除,a1有3種可能.根據乘法原理,屬於這一類的5位數有
3×10×10×9=2700(個).
⑶ 最後一個6出現在第3位,即a3=6,被3整除的數應有
3×10×9×9=2430(個).
⑷ 最後一個6出現在第2位,即a2=6,被3整除的數應有
3×9×9×9=2187(個).
⑸ a1=6,被3整除的數應有
3×9×9×9=2187(個).
根據加法原理,5位數中至少出現一個6而被3整除的數應有
3000+2700+2430+2187+2187=12504(個).
例6
在6×6的棋盤上剪下一個由四個小方格組成的凸字形,有多少種不同的剪法?
解: 我們把凸字形上面那個小方格稱為它的頭,每個凸字形有並且只有一個頭.
凸字形可以分為兩類:第一類凸字形的頭在棋盤的框線,但是棋盤的四個角是不能充當凸字形的頭的.於是,框線上(不是角)的小方格共有4×4=16個,每一個都是一個凸字形的頭,所以,這類凸字形有16個.
第二類凸字形的頭在棋盤的內部,棋盤內部的每一個小方格可以作為4個凸字形的頭(即頭朝上,頭朝下,頭朝左,頭朝右),所以,這類凸字形有
4×(4×4)=64(個).
由加法原理知,有16+64=80種不同的凸字形剪法.
練習
1.把數、理、化、語、英5本參考書,排成一行放在書架上.
⑴化學不放在第1位,共有多少種不同排法?
⑵語文與數學必須相鄰,共有多少種不同排法?
⑶物理與化學不得相鄰,共有多少種不同排法?
⑷文科書與理科書交叉排放,共有多少種不同排法?
2.在一個圓周上有10個點,把它們兩兩相連,問共有多少條不同的線段?
3.用1,2,3,4,5,6,7這七個數,
⑴可以組成多少個數字不重複的五位奇數?
⑵可以組成多少個數字不重複的五位奇數,但1不在百位上?
4.從1,2,3,4,5這五個數字中任取三個數組成一個三位數,問共可得到多少個不同的三位數?
5.由1,2,3,4,5,6這六個數字能組成多少個大於34500的五位數?
6.今有一角幣一張,兩角幣一張,伍角幣一張,一元幣四張,伍元幣兩張,用這些紙幣任意付款,可以付出不同數額的款子共有多少種?
7.將三封信投到5個郵筒中的某幾個中去,有多少種不同的投法?
8.從字母a,a,a,b,c,d,e中任選3個排成一行,共有多少種不同的排法?