含義
中間平行線即平行線中間的平行線，是和兩條平行線間的距離相等的點的軌跡，和這兩條平行線距離相等的一條平行線。
中間平行線的性質
中間平行線具有性質：
1.中間平行線上的點到兩平行線的距離相等。
2.在同一平面內，凡到兩條平行線距離相等的點必在中間平行線上，即到兩條平行線的距離相等的點的軌跡是中間平行線 。
在軌跡問題中的套用
中間平行線即平行線中間的平行線，是一種基本軌跡，即和兩條已知平行線距離相等的點的軌跡，是在兩條平行線中間而和它們距離相等的一條平行線。
這個基本軌跡套用範圍是：①求距離兩已知平行線等遠的點，②求相切於兩條已知平行線的圓的圓心。
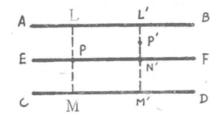圖1中間平行線軌跡的證明：
已知 EF// AB// CD，EF和AB之間的距離等於EF和CD之間的距離(圖1) 。
求證 和AB、CD距離相等的點的軌跡是EF。
證明：
(1)純粹性
設P是EF上的任何一點。經過P點作垂直於AB的直線，分別交AB、CD於L、M，那么這條直線也和CD垂直。
∵EF和AB之間的距離等於EF和CD之間的距離，
∴ PL= PM。
這就是說，EF上的任何一點和AB、CD的距離都相等。
(2)完備性
設P'是不在EF上的任何一點。
經過P'作垂直於AB的直線，分別交AB、CD、EF於L'、M'、N',那么這條直線也和CD垂直。
∵P'不在EF上，
∴P'不和N'重合。
∵ 直線L'M'上和L'、M'距離相等的點只有線段L'M'的中點N'，
∴ P'L'≠P'M'。
這就是說，不在EF上的任何一點和AB、CD的距離都不相等。
由(1)和(2)得，EF是和AB、CD距離相等的點的軌跡 。
套用舉例
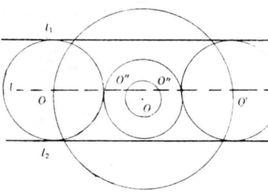
【例1】求作一圓，使它切於二已知平行線，且切於這二線間的一已知圓。
中間平行線
中間平行線已知:二直線及間的⊙O。
中間平行線求作:⊙O'使它和及⊙O都相切。
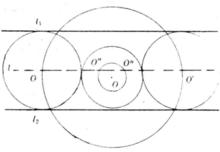圖2分析
中間平行線 中間平行線
中間平行線
中間平行線
中間平行線因為所求作的⊙O要與二平行線都相切，故其圓心的軌跡是與等距高的一條平行線，其半徑R=d/2(d為與的距離)。
中間平行線 中間平行線設⊙O的半徑為r，若⊙O'與⊙O相外切，則OO'= R十r，故O'的軌跡是以O內圓心，以R+r內半徑的大⊙O，大⊙O與的交點O'即內所求作的圓的圓心(有兩個解)，若⊙O'與OO相內切，則OO'=R-r(R>r)，故O'的軌跡是以O為圓心，以R-r內半徑的小⊙O，小⊙O與的交點O''即內所求作的圓的圓心(也有兩個解)如圖 。
