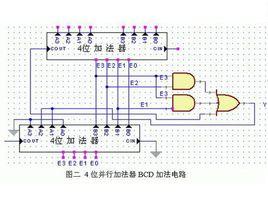
基本概念
用n位全加器實現兩個n位運算元各位同時相加,這種加法器稱為並行加法器。並行加法器中全加器的個數與運算元的位數相同。
算術邏輯單元(ALU)既能完成算術運算也能完成邏輯運算,是微處理器晶片中的一個十分重要的部件。但從基本算術運算的實現,我們可以看到所有的加、減、乘、除運算最終都能歸結為加法運算。在ALU完成的操作中,邏輯操作是按位進行,各位之間彼此無關,不存在進位問題,這使得邏輯運算速度很快,且是一個常數,不需進行過多的最佳化工作。但對於算術操作來說,因為存在進位問題,使得某一位計算結果的得出和所有低於它的位相關。因此,為了減少進位傳輸所耗的時間,提高計算速度,人們設計了多種類型的加法器,如行波進位(RIP)加法器、跳躍進位加法器(CSKA:Carry-SKip Adders)、進位選擇加法器(CSLA:Caurry-SeLect AdderS)、超前進位加法器(CLA:Carry-Lookahead Adders)等。它們都是利用各位之間的狀態(進位傳遞函式P、進位產生函式G等)來預先產生高位的進位信號,從而減少進位從低位向高位傳遞的時間。
常用設計
並行加法器中全加器的位數與運算元的位數相同,可同時對運算元的各位相加。影響運算速度的主要是傳遞進位信號的邏輯線路(即進位鏈)。根據進位鏈的不同處理方法,並行加法器又分為行波進位(RIP)加法器、先行進位加法器(CLA:Carry-Lookahead Adders)、進位選擇加法器(CSLA:Carry-SeLect Adders)和跳躍進位加法器(CSKA:Carry-SKip Adders)等。
行波進位加法器
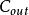 並行加法器
並行加法器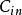 並行加法器
並行加法器行波進位加法器是將n個一位全加器串接起來進行兩個n位數的相加,進位是採用串列進位的方法來實現的,即本級的 作為下一級的 參與加法運算。其邏輯表達式為:
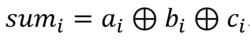 並行加法器
並行加法器同時
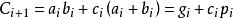 並行加法器
並行加法器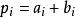 並行加法器
並行加法器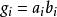 並行加法器
並行加法器所以,串列進位鏈的總延遲時間與字長成正比,字長越長,延遲時間就越長。假設每一級全加器的延遲時間為dt,則n位RIP加法器的進位總延遲為ndt。
選擇進位加法器
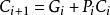 並行加法器
並行加法器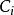 並行加法器
並行加法器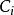 並行加法器
並行加法器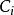 並行加法器
並行加法器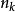 並行加法器
並行加法器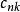 並行加法器
並行加法器根據進位計算公式 ,可以知道進位信號的得出需要依賴前級的進位信號,如果不考慮前級進位 的值,而同時計算出當 =0和 =1時向第i+1位的進位值,則所有位的進位與結果可以同時計算,等真正的進位信號產生之後,再利用它選擇出正確的結果,這種加法器就是選擇進位加法器。它是通過提高計算的並行性來改進加法器的速度的。在實際的選擇進位加法器中,為了減少等待時間,總是將n位分成K段,其中第k個段中有 位。劃分後的每個段內安排兩個加法器,同時計算向這一段的最末位的進位 是0和1兩種情況下的和,這樣各段的計算是並行的。通常這個延遲是:
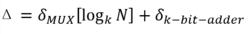 並行加法器
並行加法器一般來說,對基本的選擇進位加法器進行合理的分段可以有效地降低延遲。例如,在最低兩位(第0和第1位)採用基本的行波進位加法器,第2位和第3位再使用進位選擇加法器,假定MUX的延遲與一級進位鏈的延遲相當,那么下一個選擇進位模組的長度應該為3(第4、5、6位)。因此,進位選擇模組開始的位數為2、4、7、11、16等等。在這種情況下,加法器的延遲正比於所選擇進位模組的數目。
超前進位加法器
影響加法器速度的關鍵因素是進位信號產生和傳遞的時間,所以要想提高加法器的速度,就必須儘可能的縮短進位時間,即改進進位方式。超前進位加法器的特點是各級進位信號同時產生,大大減少了進位產生的時間。其進位產生的邏輯表達式為:
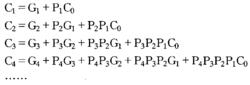 並行加法器
並行加法器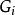 並行加法器
並行加法器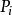 並行加法器
並行加法器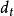 並行加法器
並行加法器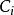 並行加法器
並行加法器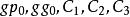 並行加法器
並行加法器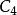 並行加法器
並行加法器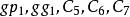 並行加法器
並行加法器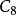 並行加法器
並行加法器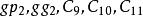 並行加法器
並行加法器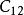 並行加法器
並行加法器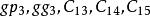 並行加法器
並行加法器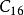 並行加法器
並行加法器從上面的表達式可知:所有各位的進位都不依賴低位的進位,每一位的進位可同時產生。若不考慮 、 的形成時間,則n位超前進位加法器的進位總延遲為 ,與字長無關。但隨著加法器位數的增加, 的表達式會越來越長,電路結構會越來越複雜,而且將受到元器件扇人係數的限制,所以完全採用並行進位是不可能的,實際上通常採用分組並行進位來實現。即把n位字長分為許多小組(每組通常4位),在組內實現先行進位,在組間既可採用RIP進位,也可採用先行進位。一般地,把組內並行,組間串列的方式稱為單級超前進位加法器;把組內並行,組間並行的方式稱為多級超前進位加法器。如16位二級超前進位加法器在實現時首先將16位劃分成四組,每組四位,第一組產生 ,不產生 ;第二組產生 ,不產生 ;第三組產生 ,不產生 ;第四組產生 ,不產生 ;其餘幾個C值用以下公式產生:
 並行加法器
並行加法器跳躍進位加法器
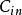 並行加法器
並行加法器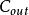 並行加法器
並行加法器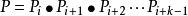 並行加法器
並行加法器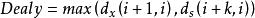 並行加法器
並行加法器超前進位加法器雖然速度很快,但它硬體支出較大。跳躍進位加法器就是在行波進位加法器的 - 路徑中,通過增加旁路邏輯來加速加法器中的進位傳遞。可以將被加數分成k位大小相等的組,在組內,進位是以行波進位的方式傳遞,利用一個位組內部的進位傳遞信號實現是否對進位輸入進行旁路的判斷, 。如果組內所有的Pi信號都是1,則進位跳旁路的條件成立,進位信號通過旁路邏輯傳遞,這可以看作是“跳躍”過了本來是串列經過的行波進位鏈的某些位,這就是跳躍進位加法器名稱的由來。在跳躍進位鏈中,假定最低位的進位Cn為0,最壞情況可能發生在以下兩種情況:一是行波進位的最壞情況,這時進位從一個組的最低位產生,傳遞到下一個組的最高位(不再向更高位傳遞,也就是該位的進位傳遞邏輯為0),跳躍進位邏輯不起作用;另一種情況是跳躍進位的最壞情況,這時進位從某個組的最低位產生,經過中問的若干組的進位跳躍邏輯後進入某個組並傳遞到該組的最高位(不再向更高位傳遞),這時跳躍進位邏輯和行波進位邏輯都起作用,整個進位鏈的時間就是所有這些情況中的最長延遲時間,即 。
16位進位跳躍加法器的結構圖如圖所示:
 並行加法器
並行加法器方法比較
加法器的性能可以從延遲、功耗、面積等方面進行分析。具體分析的方法有三種:一是通過門級模擬器來估算加法器的性能;二是採用標準單元庫對每種加法器進行邏輯綜合和布局布線來設計電路,然後從版圖中反提取電路參數,針對其參數進行電路的模擬,從中得出各種加法器的比較結果;三是通過物理實現在晶片上實現各種加法器,然後通過實際測量進行比較。
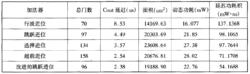
下面是加法器的比較結果:
 並行加法器
並行加法器通過對這些並行加法器的比較,可以發現行波進位加法器的速度太慢,但面積很小。選擇進位加法器使用的邏輯門數、面積較大,而速度的改善不足以補償付出的代價。延遲功耗積較小且面積相對合理的是改進後的跳躍進位加法器和超前進位加法器,其中改進後的跳躍進位加法器的延遲功耗積是最小的,而且它的面積和功耗都比超前進位加法器小,所以它具有最好的性價比。在物理實現時,超前進位加法器、跳躍進位加法器以及改進後的跳躍進位加法器的規則性較好,利於版圖實現 。