定義
考慮微分方程
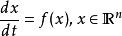 不變流形
不變流形 不變流形
不變流形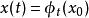 不變流形
不變流形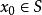 不變流形
不變流形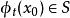 不變流形
不變流形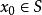 不變流形
不變流形 不變流形
不變流形 不變流形
不變流形 不變流形
不變流形設在初值 條件下的解為 。若對任意的 ,都有 (即,每條通過點 的軌道都位於集合 中),則稱 是這個系統的不變集。若 還是一個流形,則稱為不變流形。
例子
簡單2維系統
 不變流形
不變流形設 是一個確定的參數,考慮耦合微分方程組
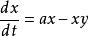 不變流形
不變流形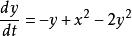 不變流形
不變流形 不變流形
不變流形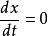 不變流形
不變流形 不變流形
不變流形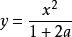 不變流形
不變流形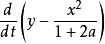 不變流形
不變流形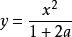 不變流形
不變流形原點是平衡點。這個系統至少有兩個過原點的不變流形。一個是垂直直線 ,因為此時 ,保證了 的值一直保持為0。另一個是拋物線 。要證明這個不變性,只需考慮時間導數 ,在 條件下保持為0即可。
非自洽動力系統的不變流形
微分方程
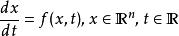 不變流形
不變流形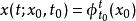 不變流形
不變流形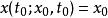 不變流形
不變流形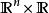 不變流形
不變流形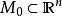 不變流形
不變流形代表了一個非自洽系統,解具有形式 ,初始條件 。在這種系統的擴展相空間 中,任何初始曲面 都能生成不變流形
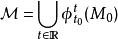 不變流形
不變流形一個基本的問題是,在這一大類不變流形中,如何確定出對整個系統的動力學影響最大的那一個。一個非自洽動力系統的擴展相空間中,最有影響的那個不變流形就是著名的拉格朗日擬序結構。
