中心流形定理

stable stable ter

定義

數學上，動態系統平衡點的中心流形（Center Manifold）是平衡點

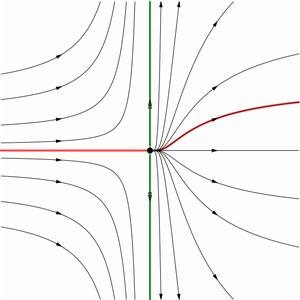鞍點附近的中心流行和不穩定不變流行

附近既不被穩定流形的吸引力（attraction of the stable manifold）控制，也不被不穩定流形的排斥力（repulsion of the unstable manifold）控制的狀態軌線。

定理

中心流形定理（Center Manifold Theorem）
控制理論中，考慮自治系統（時不變系統）dx/dt=f(x)。對其在平衡點（x*）線性化，則雅克比矩陣為 A=df/dt(x*)。中心流行定理指出，如果f(x)是r階連續可導，則在任意平衡點，存在唯一的 r 階連續可導的穩定流形，存在唯一的 r 階連續可導的不穩定流形，並存在（不一定唯一）r-1 階連續可導的中心流形。

套用

中心流行定理在分岔理論中有重要的套用。
對於上述n維非線性動態系統，當其雅克比矩陣A只具有零實部和負實部的特徵值時，平衡點演變為n維空間的光滑子空間，比如3維空間中的面和線。這樣，則無法通過線性化來確定其在平衡點（流形）附近的穩定性。中心流形定理可以通過分析與原系統對應的低階系統進而確定原系統在平衡點附近的穩定性，而該對應低階系統的階數恰好是A具有的零實部特徵值的個數。