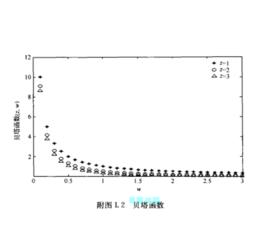
貝塔函式簡介
在機率統計和其他套用學科中會經常用到伽瑪函式和貝塔函式,有的反常積分的計算最後也會歸結為貝塔函式或伽瑪函式。 貝塔函式又稱為第一類歐拉積分,伽瑪函式也可稱為第二類歐拉積分。
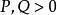 貝塔函式
貝塔函式對任意實數
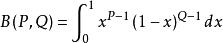 貝塔函式
貝塔函式稱該函式為貝塔函式,或 Beta 函式,B 函式。
 貝塔函式
貝塔函式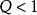 貝塔函式
貝塔函式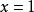 貝塔函式
貝塔函式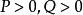 貝塔函式
貝塔函式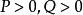 貝塔函式
貝塔函式當P<1 時,是以 為瑕點的無界函式反常積分;當 時,是以 為瑕點的無界函式反常積分,套用柯西判別法可證得當 時,這兩個無界函式反常積分都收斂,所以貝塔函式的定義域為 。
貝塔函式性質
連續性
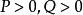 貝塔函式
貝塔函式貝塔函式在定義域 內連續。
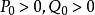 貝塔函式
貝塔函式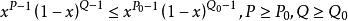 貝塔函式
貝塔函式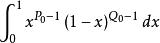 貝塔函式
貝塔函式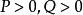 貝塔函式
貝塔函式證明:由於對任何 成立不等式 ,而積分 收斂,故由魏爾斯特拉斯 M 判別法可知貝塔函式在定義域 內連續。
對稱性
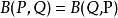 貝塔函式
貝塔函式推導過程:
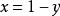 貝塔函式
貝塔函式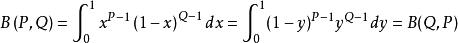 貝塔函式
貝塔函式令 ,得: 。
遞推公式
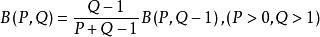 貝塔函式
貝塔函式(1) ;
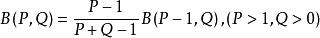 貝塔函式
貝塔函式(2) ;
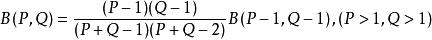 貝塔函式
貝塔函式(3) 。
近似公式
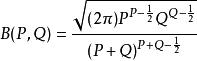 貝塔函式
貝塔函式根據斯泰林公式,當P,Q比較大時,我們有近似公式 。
其他形式
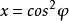 貝塔函式
貝塔函式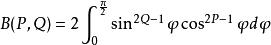 貝塔函式
貝塔函式(1)令 ,則有: 。
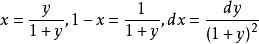 貝塔函式
貝塔函式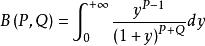 貝塔函式
貝塔函式(2)令 ,則有 。
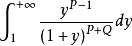 貝塔函式
貝塔函式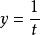 貝塔函式
貝塔函式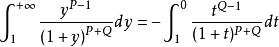 貝塔函式
貝塔函式(3)考察 ,令 ,則有: ,
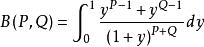 貝塔函式
貝塔函式故有: 。
與其它函式
與伽瑪函式的關係
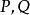 貝塔函式
貝塔函式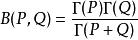 貝塔函式
貝塔函式(1)對於任意的正實數 ,有關係表達式: 。
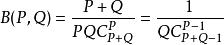 貝塔函式
貝塔函式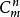 貝塔函式
貝塔函式(2)當P、Q都是正整數時,我們可以將結果寫成 ,其中 是二項式係數。
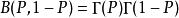 貝塔函式
貝塔函式(3) 。
與不完全貝塔函式關係
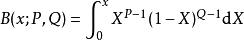 貝塔函式
貝塔函式(1) ,很顯然當 x 取1時,結果就變成完全的貝塔函式了。
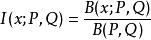 貝塔函式
貝塔函式(2)不完全貝塔函式和對應貝塔函式的比值 構成了歸一化的貝塔函式。而它正好是滿足貝塔分布的隨機變數的分布函式。