不可解度
正文
從比較計算難易程度出發來研究自然數子集分類的遞歸論分支。在某種標準下計算難度相同的集合形成這種標準下的一個度。遞歸論中研究得比較多的兩種度是m度與圖靈度。設A與B是兩個非負整數的子集,假若存在遞歸函式ƒ使得
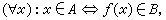
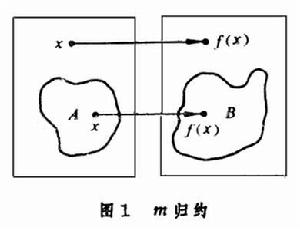 )並記為
)並記為 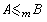 。
。
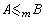 且
且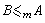 ,則稱A與B是m等價的並記為
,則稱A與B是m等價的並記為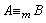 ,類
,類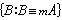 被稱為A的m度。假若B是遞歸可枚舉集且任何遞歸可枚舉集A都可m歸約於B,則稱B是m完備的。關於圖靈機停機問題的集合
被稱為A的m度。假若B是遞歸可枚舉集且任何遞歸可枚舉集A都可m歸約於B,則稱B是m完備的。關於圖靈機停機問題的集合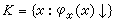 就是一個m完備集。
就是一個m完備集。 設B的補集為峫,要判定元素x在不在峫中,只要判定x在不在B中就可以了,因此直觀上峫應該可歸約於B。但是上面給出的m歸約辦不到這一點。例如,噖 不可m 歸約於K。因此需要有新的更一般的歸約標準,圖靈歸約(見圖2
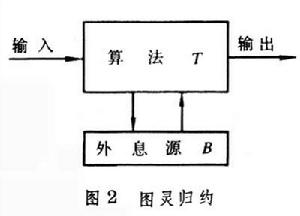 )是其中最重要的一個。
)是其中最重要的一個。 稱“A圖靈歸約於B”(或“A遞歸於B”,或“A相對於B可計算”)是指:有一個算法 T,當輸入非負整數x時,依據該算法進行的計算過程中,可以隨時向外息源詢問“y是否屬於B”這樣的問題,並根據外息源的回答來決定下一步計算怎樣進行,直到給出x是否屬於A時為止。
用“
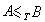 ”表示"A圖靈歸約於B",用“
”表示"A圖靈歸約於B",用“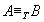 ”表示 “
”表示 “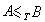 且
且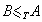 ”。記
”。記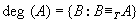 並稱其為 A的圖靈度。若
並稱其為 A的圖靈度。若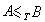 則記作deg(A)≤deg(B)。若deg(A)≤deg(B)但
則記作deg(A)≤deg(B)。若deg(A)≤deg(B)但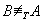 則記作deg(A)B)。若
則記作deg(A)B)。若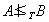 且
且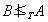 則稱deg(A)與deg(B)為不可比度。若B是遞歸可枚舉集且對任何遞歸可枚舉集A都有A≤iB,則稱B是(圖靈)完備集。K與噖 是完備集。
則稱deg(A)與deg(B)為不可比度。若B是遞歸可枚舉集且對任何遞歸可枚舉集A都有A≤iB,則稱B是(圖靈)完備集。K與噖 是完備集。 一切遞歸集形成一個度,用Ο表示遞歸集的度。因為任何集 B與遞歸集A有關係
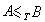 ,所以對任何度a都有Ο≤a,即Ο是最小的度。用Ο┡表示完備集K的度,顯然任何完備集都在度Ο┡中。因為K不是遞歸集,故有Ο<Ο┡。用【Ο,Ο┡】表示度類{a:Ο≤a≤Ο┡}。
,所以對任何度a都有Ο≤a,即Ο是最小的度。用Ο┡表示完備集K的度,顯然任何完備集都在度Ο┡中。因為K不是遞歸集,故有Ο<Ο┡。用【Ο,Ο┡】表示度類{a:Ο≤a≤Ο┡}。 一個度中若有一個遞歸可枚舉集,則稱這個度為遞歸可枚舉度。因為Ο┡是完備集的度,所以對任何遞歸可枚舉度a都有Ο≤a≤Ο┡。是否有遞歸可枚舉度a使Ο<a<Ο┡呢?這個問題是遞歸論中有名的波斯特問題。1956~1957年,A.A.穆切尼克與R.M.弗里德貝格創造了有窮損害方法證明了在【Ο,Ο┡】中有兩個互不可比的遞歸可枚舉度,從而肯定地解決了波斯特問題。
稱集合
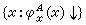 為集合A的躍變,把A的躍變記為A┡。 度a=deg(A)的躍變度記為 a┡=deg(A┡)。度Ο的躍變度是Ο┡。對於任何遞歸可枚舉度a,它的躍變度a┡滿足Ο┡≤a┡≤Ο″,若有Ο┡=a┡則稱遞歸可枚舉度 a為低度,若有Ο″=a┡則稱a為高度。
為集合A的躍變,把A的躍變記為A┡。 度a=deg(A)的躍變度記為 a┡=deg(A┡)。度Ο的躍變度是Ο┡。對於任何遞歸可枚舉度a,它的躍變度a┡滿足Ο┡≤a┡≤Ο″,若有Ο┡=a┡則稱遞歸可枚舉度 a為低度,若有Ο″=a┡則稱a為高度。 存在度α使Ο<α<Ο┡且對任何度b若b≠Ο則b≮α,這樣的度a叫極小度。不存在非Ο的遞歸可枚舉度是極小度。【Ο,Ο┡】的基數與實數區間【0,1】的基數相同,【Ο,Ο┡】也存在類似的稠密性質。【Ο,Ο┡】是上半格但不是格,每一個可數分配格都可嵌入 【Ο,Ο┡】中。存在一對非Ο的遞歸可枚舉度,它們的最大下界是Ο;不存在一對非Ο的遞歸可枚舉度,它們的最大下界是Ο而最小上界則是Ο┡。
研究在【Ο,Ο┡】上的偏序性質特別是代數結構性質是不可解度理論的重要內容。