定義
定義：若矩陣 L具有下列形式：
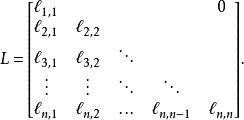下三角矩陣則稱為下三角矩陣 。
若矩陣 U具有下列形式：
下三角矩陣則稱為上三角矩陣。
許多矩陣運算保持下三角性不變:
•兩個下三角矩陣的和下三角。
•兩個下三角矩陣的乘積是下三角。
•一個可逆的下三角矩陣的逆是下三角。
•下三角矩陣與常數相乘是一個下三角矩陣。
•以上性質對上三角矩陣也成立。
嚴格上(下)三角矩陣
若上（下）三角矩陣對角線元素全是1，則稱為嚴格上（下）三角矩陣。
原子三角矩陣
一個原子下(上)三角矩陣是矩陣的一種特殊形式，所有的地方非對角元素為零，除了在單個列的條目。這樣一個矩陣也被稱為弗羅貝尼烏斯矩陣，高斯矩陣或高斯變換矩陣。即原子下三角矩陣的形式
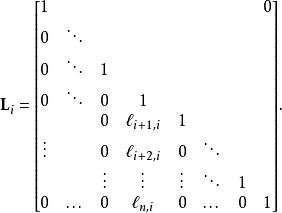下三角矩陣一個原子三角矩陣的逆再次原子三角形。事實上，我們有
下三角矩陣例子
下三角矩陣是上三角陣。
下三角矩陣是下三角陣
下三角矩陣是原子下三角矩陣，其逆為
下三角矩陣方程組求解
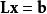下三角矩陣
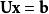下三角矩陣一個矩陣方程形式 或 很容易解決的一個疊代過程給出求解。
Lx = b矩陣方程可以寫成一個線性方程組
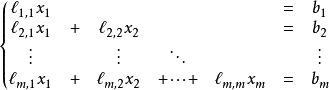下三角矩陣其解疊代公式 為
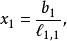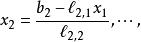下三角矩陣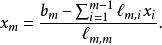
下三角矩陣
下三角矩陣算法
下面給出一個C語言的算法實現：
public static double[] luEvaluate(double[][] L, double[][] U, double[] b)
{
// Ax = b -> LUx = b. Then y is defined to be Ux
double[] x = new double[b.Length];
double[] y = new double[b.Length];
// Forward solve Ly = b
for (int i = 0; i < b.Length; i++)
{
y[i] = b[i];
for (int j = 0; j < i; j++) {
y[i] -= L[i][j] * y[j];
}
y[i] /= L[i][i];
}
// Backward solve Ux = y
for (int i = b.Length - 1; i >= 0; i--)
{
x[i] = y[i];
for (int j = i + 1; j < n; j++) {
x[i] -= U[i][j] * x[j];
}
x[i] /= U[i][i];
}
return x;
}
