基本介紹
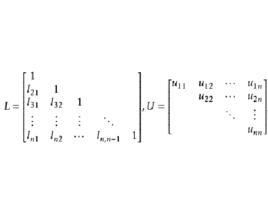
若能通過正交變換,將係數矩陣A分解為A=LU,其中L是單位下三角矩陣(主對角線元素為1的下三角矩陣),而U是上三角矩陣,則線性方程組Ax=b變為LUx=b,若令Ux=y,則線性方程組Ax=b的求解分為兩個三角方程組的求解:
(1)求解Ly=b,得y;
(2)再求解Ux=y,即得方程組的解x;
因此三角分解法的關鍵問題在於係數矩陣 A的LU分解。
矩陣能LU分解的充分條件
一般地,任給一個矩陣不一定有LU分解,下面給出一個矩陣能LU分解的充分條件。
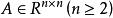 三角分解法
三角分解法定理1 對任意矩陣 ,若A的各階順序主子式均不為零,則A有唯一的Doolittle分解(或Crout分解)。
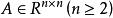 三角分解法
三角分解法定理2 若矩陣 非奇異,且其LU分解存在,則A的LU分解是唯一的。
矩陣A的Doolittle分解
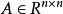 三角分解法
三角分解法定義1 設 ,稱A=LU,其中
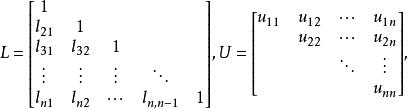 三角分解法
三角分解法為矩陣A的 Doolittle分解(Doolittle factorization或Doolittle decomposition)。
矩陣的Doolittle分解可以通過Gauss消去法或直接利用矩陣的乘法得到。
假設A的各階順序主子式均不為零,從Gauss消去法的消元過程可以看出,第一次消元時執行了n一1次初等行變換,若用矩陣的語言解釋,相當於
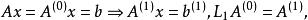 三角分解法
三角分解法其中
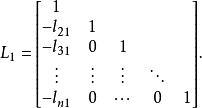 三角分解法
三角分解法第二次消元時,相當於
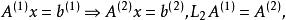 三角分解法
三角分解法其中
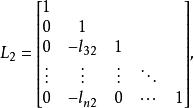 三角分解法
三角分解法重複上述過程,經過n一1次消元,最後得到等價方程組:
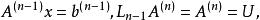 三角分解法
三角分解法其中
 三角分解法
三角分解法綜上所述,得
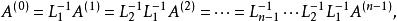 三角分解法
三角分解法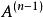 三角分解法
三角分解法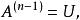 三角分解法
三角分解法而 為上三角矩陣,記 且
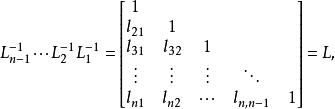 三角分解法
三角分解法於是有
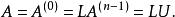 三角分解法
三角分解法註上述過程中,若不假設A的各階順序主子式均不為零,只假設A非奇異,則Gauss消元過程未必能完全實施,一般需要選主元,然後進行初等行或列變換,以保證消元過程的進行.若用矩陣的語言解釋,相當於對A左乘或右乘一個置換矩陣。
定理3 若A非奇異,則一定存在置換矩陣(permutation matrix)P,使得PA有三角分解PA=LU,其中L是單位下三角矩陣(主對角線元素為1的下三角矩陣),而U是上三角矩陣。
由定理1知,存在矩陣P使得線性方程組PAx=Pb化為LUx=Pb,進而由
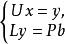 三角分解法
三角分解法求得原方程組的解x。
若直接利用矩陣乘法,可設
 三角分解法
三角分解法由矩陣相等的定義,得L與U的遞推計算公式如下:
(1) U的第一行、L的第一列的元素分別為
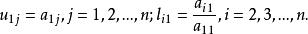 三角分解法
三角分解法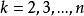 三角分解法
三角分解法(2) 對 (依次:U的第二行,L的第二列,U的第三行,L的第三列……),有
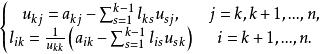 三角分解法
三角分解法由上述兩種方法得到矩陣A的LU分解後,求解Ly=b與Ux=y的計算公式為
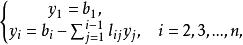 三角分解法
三角分解法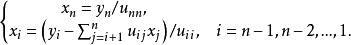 三角分解法
三角分解法