交錯級數
若級數的各項符號正負相間，即
一般項級數則稱（1）為交錯級數。
對於交錯級數，有下面常用的判別法。
定理1（萊布尼茨判別法）
若交錯級數（1）滿足下述兩個條件：
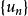一般項級數（i）數列 單調遞減；
一般項級數（ii）
則級數（1）收斂 。
推論1
若級數（1）滿足萊布尼茨判別法的條件，則收斂級數（1）的餘項估計式為
一般項級數對於下列交錯級數套用萊布尼茨判別法檢驗，容易檢驗它們都是收斂的。
一般項級數
一般項級數
一般項級數絕對收斂級數及其性質
若級數
一般項級數各項絕對值所組成的級數
一般項級數收斂，則稱原級數（2）為絕對收斂級數。
定理2
絕對收斂級數一定收斂 。
例1
級數
一般項級數的各項絕對值所組成的級數是
一般項級數
一般項級數套用比式判別法，對於任何實數都有
一般項級數 一般項級數因此，所考察的級數對任何實數都絕對收斂。
若級數（5）收斂，但級數（6）不收斂，則稱級數（5）為條件收斂級數。
例如級數（2）是條件收斂，而級數（3）、（4）則是絕對收斂。
全體收斂的級數可分為絕對收斂級數與條件收斂級數兩大類。
阿貝爾判別法和狄利克雷判別法
下面討論級數
一般項級數收斂性的判別法。
定理3（阿貝爾判別法）
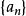一般項級數
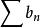一般項級數若為單調有界數列，且級數收斂，則級數（7）收斂。
定理4（狄利克雷判別法）
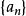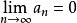一般項級數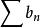
一般項級數 一般項級數若數列單調遞減，且，又級數的部分和數列有界，則級數（7）收斂。
