概念
一致連續映射(uniformly continuous mapping)是一致空間上的一類重要映射。設(X，U)，(Y，V)是兩個一致空間，f：X→Y。若對於任意V∈V，存在U∈U使得當(x，y)∈U時有(f(x)，f(y))∈V，則稱f關於U和V是一致連續的，簡稱f是一致連續映射。兩個一致連續映射的複合映射是一致連續的。每個一致連續映射關於一致拓撲是連續的。若(X，U)關於一致拓撲是緊的，則所有連續映射f：X→Y是一致連續的。
映射
映射亦稱函式。數學的基本概念之一。也是一種特殊的關係。設G是從X到Y的關係，G的定義域D(G)為X，且對任何x∈X都有惟一的y∈Y滿足G(x，y)，則稱G為從X到Y的映射。即關係G為映射時，應滿足下列兩個條件：
1.(x∈X)(y∈Y)(xGy).
2.(x∈X)(y∈Y)(z∈Y)((xGy∧xGz)→y=z).這個被x∈X所惟一確定的y∈Y，通常表示為y=f(x)(x∈X).f(x)滿足：
1) f(x)∈Y.
2) G(x，f(x))成立(x∈X).
3)z∈Y，G(x，z)→z=f(x).
關係G常使用另一些記號：f：X→Y或XY.f與G的關係是y=f(x)(x∈X)，若且唯若G(x，y)成立。可取變域X中的不同元素為值的變元稱為自變元或自變數。同樣可取變域Y中的不同元素為值的變元稱為因變元或因變數。始集X稱為映射f的定義域。記為D(f)或dom(f)。終集Y稱為映射的陪域，記為C(f)或codom(f)。Y中與X中的元素有關係G的元素的組合{y|x(x∈X∧y=f(x)∈Y)}稱為映射的值域，記為R(f)或ran(f)。當y=f(x)時，y稱為x的象，而x稱為y的原象。y的所有原象所成之集用f(y)表示。對於AX，所有A中元素的象的集合{y|x(x∈A∧y=f(x)∈Y)}或{f(x)|x∈A}稱為A的象。記為f(A)。對於BY，所有B中元素的原象的集合{x|x∈X∧y(y∈B∧y=f(x))}稱為B的原象。記為f(B)。顯然：f(A)=f(x)，f(B)=f(y)。
一致空間
一致空間是一致結構上的空間。一致結構是指集合上的一種結構。設X為集合，U為X×X的非空子集族。若U滿足下列條件，則稱U是X上的一致結構：
1.U的每一個元包含對角線Δ.
2.若U∈U，則U∈U，其中
U={(x，y)|(y，x)∈U}.
3.若U∈U，則存在V∈U使得V°VU，其中
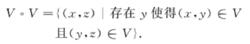一致連續映射4.若U，V∈U，則U∩V∈U.
5.若U∈U並且UVX×X，則V∈U.
具有一致結構U的集合X稱為一致空間，記為(X，U)。一致空間的概念是韋伊(Weil，A.)於1938年引入的。布爾巴基(Bourbaki，N.)於1940年首先給予系統的論述。圖基(Tukey，J.W.)於1940年用覆蓋族定義並研究了一致空間的等價的概念。艾斯貝爾(Isbell，J.R.)於1964年出版的書中，包含了用覆蓋敘述的一致空間理論的重要發展。一致空間也可用偽度量族來描述，它是由布爾巴基於1948年給出的。
一致拓撲
一致拓撲是由一致結構誘導的拓撲。設(X，U)為一致空間，T是X的子集，滿足：對於任意x∈T，存在U∈U使得U(x)T，其中U(x)={y|(x，y)∈U}。所有這種T組成的集族T是X上的一個拓撲，稱為由一致結構U誘導的拓撲或一致拓撲。當由一致結構U誘導的拓撲空間X為緊空間時，則和X的拓撲一致的一致結構是惟一確定的。一致空間是完全正則的，並且完全正則空間具有和它的拓撲一致的一致拓撲。即有下述結果：集合X上的拓撲T為X上的某個一致結構的一致拓撲的充分必要條件是，(X，T)為完全正則空間。
一致連續
一致連續亦稱均勻連續。反映函式均勻變化的性質。設f是從集合ER到R的實函式，若對任意ε>0，存在δ>0，使：
sup{|f(x)-f(x)|x，x∈E，|x-x|<δ}<ε，
或對x，x∈E，|x-x|<δ，有|f(x)-f(x)|<ε，則f稱為在E上一致連續。函式f∶E(R)→R一致連續的定義可完全類似給出，只要把|·|理解為R或R中的範數|·|.相對於一致連續，把f在E上連續稱為逐點連續。一致連續函式必逐點連續，反之不一定.但在R的有界閉集上連續的函式必一致連續。若f定義在開區間(a，b)上，則f一致連續若且唯若f連續，且f(a+)與f(b-)存在且有限。例如，對函式g(x)=1/x，有g(0+)=+∞，故g不在(0，+∞)上一致連續。一致連續函式把柯西列映為柯西列，即若f一致連續，{x}是柯西列，則{f(x)}也是柯西列；反之，定義在有界集上，把柯西列映為柯西列的函式必一致連續。一致連續函式的線性組合一致連續。兩個一致連續函式的複合函式一致連續。一致連續性是由海涅(Heine，H.E.)於1870年引入的。
