一致有界性

簡介

一致有界性是指一個函式族中的函式有共同的界。

一致有界的函式族中每個函式均有界，反之不然。

一致有界

設={f}是定義在集A上的實值函式族，若存在數M，使對所有λ∈及x∈A有f(x)≤M，則稱在A上一致有上界，並稱M為其一致上界。

類似的，可定義一致有下界及一致下界。即存在數M，使對所有λ∈及x∈A有f(x)≥M，則稱在A上一致有下界，並稱M為其一致下界。

若既一致有上界又一致有下界，即存在M>0，使對所有λ∈及x∈A有|f(x)|≤M，則稱（在A上）一致有界，並稱M為（在A上）的一致界。

一致有界性定理

一致有界性定理又稱共鳴定理。

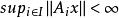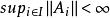一致有界性

一致有界性

設￡為Banach空間，M為賦范線性空間，{A,i∈I}為L→M的有界線性運算元族。若∀x∈L，，則。