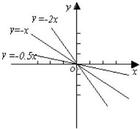
基本信息
1.y的變化值與對應的x的變化值成正比例,比值為k即:△y/△x=k (△為任意不為零的實數),即函式圖像的斜率。
2. 一次函式的表達式:f(x)=kx+b
3.性質:當k>0時,y隨x的增大而增大;
當k<0時,y隨x的增大而減小。
當b>0時,該函式與y軸交於正半軸;
當b<0時,該函式與y軸交於負半軸
當x=0時,b為函式在y軸上的截距。
4.一次函式定義域x∈R,值域f(x)∈R
5.一次函式在x∈R上的單調性:
若f(x)=kx+b,k>0,則該函式在x∈R上單調遞增。
若f(x)=kx+b,k<0,則該函式在x∈R上單調遞減。
函式性質
1.y的變化值與對應的x的變化值成正比例,比值為k即:y=kx+b(k≠0) (k不等於0,且k,b為常數)
2.當x=0時,b為函式在y軸上的,坐標為(0,b).
當y=0時,該函式圖像在x軸上的交點坐標為(-b/k,0)
3.k為一次函式y=kx+b的斜率,k=tanΘ(角Θ為一次函式圖象與x軸正方向夾角,Θ≠90°)
形、取、象、交、減。
4.當b=0時(即 y=kx),一次函式圖像變為正比例函式,正比例函式是特殊的一次函式.
5.函式圖像性質:當k相同,且b不相等,圖像平行;
6當k不同,且b相等,圖像相交;
7當k互為負倒數時,兩直線垂直;
8當k,b都相同時,兩條直線重合。
圖像性質
1.作法與圖形:通過如下3個步驟(1)列表
(2)描點;[一般取兩個點,根據“兩點確定一條直線”的道理];
(3)連線,可以作出一次函式的圖像——一條直線。因此,作一次函式的圖像只需知道2點,並連成直線即可。(通常找函式圖像與x軸和y軸的交點分別是-k分之b與0,0與b)
2.性質:(1)在一次函式上的任意一點P(x,y),都滿足等式:y=kx+b(k≠0)。(2)一次函式與y軸交點的坐標總是(0,b),與x軸總是交於(-b/k,0)正比例函式的圖像都是過原點。
3.函式不是數,它是指某一變化過程中兩個變數之間的關係。
4.k,b與函式圖像所在象限:
y=kx時(即b等於0,y與x成正比,此時的圖像是是一條經過原點的直線)
當k>0時,直線必通過一、三象限,y隨x的增大而增大;
當k<0時,直線必通過二、四象限,y隨x的增大而減小。
y=kx+b(k,b為常數,k≠0)時:
當 k>0,b>0, 這時此函式的圖象經過一,二,三象限。
當 k>0,b<0, 這時此函式的圖象經過一,三,四象限。
當 k<0,b>0, 這時此函式的圖象經過一,二,四象限。
當 k<0,b<0, 這時此函式的圖象經過二,三,四象限。
當b>0時,直線必通過一、二象限;
當b<0時,直線必通過三、四象限。
特別地,當b=0時,直線通過原點O(0,0)表示的是正比例函式的圖像。
這時,當k>0時,直線只通過一、三象限,不會通過二、四象限。當k<0時,直線只通過二、四象限,不會通過一、三象限。
4、特殊位置關係
當平面直角坐標系中兩直線平行時,其函式解析式中K值(即一次項係數)相等.
當平面直角坐標系中兩直線垂直時,其函式解析式中K值互為負倒數(即兩個K值的乘積為-1).