介紹
數獨(日語:數獨 すうどく)是一種源自18世紀末的瑞士,後在美國發展、並在日本得以發揚光大的數學智力拚圖遊戲。拼圖是九宮格(即3格寬×3格高)的正方形狀,每一格又細分為一個九宮格。在每一個小九宮格中,分別填上1至9的數字,讓整個大九宮格每一列、每一行的數字都不重複。
數獨的玩法
邏輯簡單,數字排列方式千變萬化。不少教育者認為數獨是鍛鍊腦筋的好方法。
歷史
如今數獨的雛型首先於1970年代由美國的一家數學邏輯游戲雜誌發表,當時名為NumberPlace。現今流行的數獨於1984年由日本遊戲雜誌《パズル通信ニコリ》發表並得了現時的名稱。數獨本是“獨立的數字”的省略,因為每一個方格都填上一個個位數。
數獨衝出日本成為英國當下的流行遊戲,多得曾任香港高等法院法官的高樂德(WayneGould)。2004年,他在日本旅行的時候,發現雜誌的這款遊戲,便帶回倫敦向《泰晤士報》推介並獲得接納。英國《每日郵報》也於三日後開始連載,使數獨在英國正式掀起熱潮。其他國家和地區受其影響也開始連載數獨。
數獨術語
要理解如何對一個數獨題求解,我們先來介紹一些在本網站中使用的術語。
單元格和值
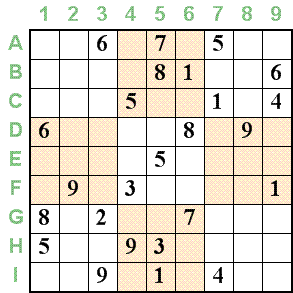 《數獨》
《數獨》行和列。習慣上,橫為行,縱為列,在這裡也不例外。行由橫向的9個單元格組成,而列由縱向的9個單元格組成。很明顯,整個謎題由9行和9列組成。為了避免混淆,這裡用大寫英文字母和數字分別表示行和列。例如,單元格[G6]指的是行G和第6列交界處的單元格,它已填入了值7。
區塊
術語區塊指的是起始於特定位置的9個相鄰的單元格組。在上圖中,區塊用交替相間的背景顏色來註明。例如,對於最左上角的區塊,我們表示為起始於[A1]的區塊。
單元
任何一行,一列或一個區塊都是一個單元。每個單元都必須包含全部但不重複的數字1到9。
數獨題目難度
很多人認為數獨題目的難度取決於已填入謎題中的數字的數量,其實這並不盡然。一般來說,填入的數字越多,題目就越容易求解。然而實際上,有很多填入數字多的題目比填入數字少的題目要難得多。這就需要有其他的方法來確定的難度。在套用中使用得比較多的一種方法是看看要解決一道數獨題目需要用到哪些數獨技巧。極簡單的題目用到的可能只是最基本的技巧。而相對複雜的題目可能要用到十分高深的解題方法。通過這樣來設定遊戲的難度相對而言較為客觀。
數獨的變化
人們總是不滿足於已有的一切。同樣,對於普遍使用的9x9謎題而言,大量湧現的變形數獨題也在不斷豐富著數獨家族。
一種比較常見的數獨變形是大小上的改變。現在已有的大小包括:4x4,6x6,12x12,16x16,25x25,甚至還有100x100。
另一種數獨變形題是在原數獨規則的基礎上加入其他的規則。譬如X形數獨就要求除原來的數獨規則外,連主對角線上的單元格也要滿足數字1到9的唯一性和完整性。而殺手數獨則要求每個“區”(虛線環繞的一組單元格)中的值必須唯一且總和等於區的右上角所指定的數字。
