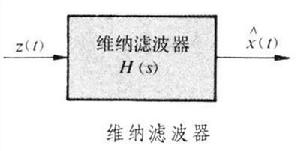
Wiener filtering
利用平穩隨機過程的相關特性和頻譜特性對混有噪聲的信號進行濾波的方法,1942年美國科學家N.維納為解決對空射擊的控制問題所建立。維納濾波是40年代線上性濾波理論方面所取得的最重要的成果。
濾波問題 用x(t)表示信號的真實值,n(t)表示噪聲,其中t表示時間,則實際上觀測到的信號是
z(t)=x(t)+n(t)
濾波就是要從實測信號z(t)中儘可能濾掉噪聲n(t),以得到真實信號x(t)的良好估值。數學上,濾波問題可以歸結為根據z(t)來求出x(t)的最優估值x(t)(即上圖中的輸出信號x尖尖)。
維納濾波中,最優估值x(t)是在均方誤差的數學期望E[x(t)-x(t)]2取極小意義下的一種估值。在假定信號過程x(t)與噪聲過程n(t)為聯合平穩和假定在半無限時間區間(-∞,t)內能獲得z(t)的全部觀測數據的前提下,維納濾波給出了計算最優估值x(t)的一種方法。
維納濾波器 實現維納濾波方法的系統或裝置稱為維納濾波器。維納濾波器在結構上是一個定常線性系統(見圖),通過合理的設計可使其對噪聲n(t)具有良好的過濾特性。當觀測信號z(t)=x(t)+n(t)輸入濾波器時,它的輸出就是信號x(t)的最優估值x(t)。
構造維納濾波器的步驟 假設維納濾波器的單位脈衝回響函式是h(t),則最優估值x(t)的關係式為
如用Rxz(τ)表示x(t)和z(t)的互相關函式,Rzz(τ)表示z(t)的自相關函式,那么業已證明它們之間具有類似於上式的關係式
這個關係式稱為維納-霍夫方程。如果所討論的各隨機過程均具有各態歷經性,則式中的Rxz(τ)和Rzz(τ)均是已知的。設計維納濾波器的問題,可歸結為從維納-霍夫積分方程中解出未知函式h(t)。h(t)的拉普拉斯變換就是所要決定的維納濾波器的傳遞函式H(s)。對於一般問題,維納-霍夫方程往往不易求解。但當給定問題的隨機過程的功率譜密度是有理分式函式時,H(s)的顯式解就可比較容易地定出。根據求得的H(s)即可構造所需的維納濾波器,而信號的最優估值憫(t)則可由相應關係式定出。
維納濾波器的優缺點 維納濾波器的優點是適應面較廣,無論平穩隨機過程是連續的還是離散的,是標量的還是向量的,都可套用。對某些問題,還可求出濾波器傳遞函式的顯式解,並進而採用由簡單的物理元件組成的網路構成維納濾波器。維納濾波器的缺點是,要求得到半無限時間區間內的全部觀察數據的條件很難滿足,同時它也不能用於噪聲n(t)為非平穩的隨機過程的情況,對於向量情況套用也不方便。因此,維納濾波在實際問題中套用不多。
參考書目
錢學森、宋健:《工程控制論》(下冊),科學出版社,北京,1981。
Y.W.Lee, Statistical Theory of Communication, John Wiley and Sons,Inc.,New York,1960.
