Tan[正切]

Tan是正切的意思，角θ在任意直角三角形中，與θ相對應的對邊與鄰邊的比值叫做角θ的正切值 。若將θ放在直角坐標系中即tanθ=y/x。tanA=對邊/鄰邊。在直角坐標系中相當於直線的斜率k。

基本信息

• 中文名：正切
• 其他外文名：tangent

• 別稱：tan.
• 套用學科：數學、物理、
• 適用領域範圍：坡度計算

定義

正切函式是直角三角形中，對邊與鄰邊的比值叫做正切。放在直角坐標系中（如圖）即 tanθ=y/x

Tan 取某個角並返回直角三角形兩個直角邊的比值。此比值是直角三角形中該角的對邊長度與鄰邊長度之比，也可寫作tg。

正切tangent，因此在上世紀九十年代以前正切函式是用tgθ來表示的，而現在用tanθ來表示。

將角度乘以 π/180 即可轉換為弧度，將弧度乘以 180/π 即可轉換為角度。

Tan[正切]

在三角函式中： ； tanθ=1/cotθ.

在Rt△ABC，∠C=90度，AB=c,BC=a,AC=b,tanA=BC/AC=a/b

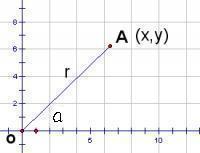
Tan[正切]

將一個角放入直角坐標系中 使角的始邊與X軸的非負半軸重合

在角的終邊上找一點A（x，y）

過A做X軸的垂線

則r=(x^2+y^2）^（1/2）

tan =y/x

正切無最大最小值。

tanA=∠A的對邊/∠A的鄰邊

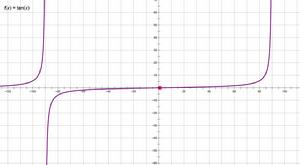函式圖像

30°　sinα=1/2　cosα=√3/2　tanα=√3/3

Tan[正切]

Tan[正切]

45°　sinα= 　cosα= 　tanα=1

Tan[正切]

60°　sinα= cosα=1/2　tanα=√3

90°　sinα=1　cosα=0　tanα不存在

Tan[正切]

120°　sinα=√3/2　cosα=-1/2　tanα=-√3

150°　sinα=1/2　cosα=-√3/2　tanα=-√3/3

180°　sinα=0　cosα=-1　tanα=0

270°　sinα=-1　cosα=0　tanα不存在

360°　sinα=0　cosα=1　tanα=0

公式

幾個常用公式：

tan a=sin a/cos a

tanα=1/cotα

1、設α為任意角，終邊相同的角的同一三角函式的值相等：tan（2kπ+α）=tanα

2、設α為任意角，π+α的三角函式值與α的三角函式值之間的關係：tan（π+α）=tanα

3、任意角α與 -α的三角函式值之間的關係： tan（－α）=－tanα

4、利用公式二和公式三可以得到π-α與α的三角函式值之間的關係：tan（π－α）=－tanα

5、利用公式一和公式三可以得到2π-α與α的三角函式值之間的關係：tan（2π－α）=－tanα

6、π/2±α及3π/2±α與α的三角函式值之間的關係：

tan（π/2+α）=－cotα

tan（π/2－α）=cotα

tan（3π/2+α）=－cotα

tan（3π/2－α）=cotα(以上k∈Z)

一般的最常用公式

口訣;奇變偶不變，符號看象限 一般的最常用公式有:

Sin(A+B)=SinA*CosB+SinB*CosA Sin(A-B)=SinA*CosB-SinB*CosA Cos(A+B)=CosA*CosB-SinA*SinB Cos(A-B)=CosA*CosB+SinA*SinB

Tan(A+B)=(TanA+TanB)/(1-TanA*TanB) Tan(A-B)=(TanA-TanB)/(1+TanA*TanB) 同角三角函式的關係（即同角八式） ·平方關係

·平方關係：

sin^2(α)+cos^2(α)=1 tan^2(α)+1=sec^2(α) cot^2(α)+1=csc^2(α)

誘導公式

tan（2kπ+α）=tan α

tan(π/2-α）=cot α

tan（π/2+α）=-cot α

tan（π+α）=tan α

tan（π-α）=-tan α

兩角和差公式

正切示意圖

tan（α+β）=(tanα+tanβ）/（1-tanα·tanβ）

tan（α-β）=(tanα-tanβ）/（1+tanα·tanβ）

tan(a+b+c)=tanα+tanb+tanc-tanatanbtanc/1-tanatanb-tanctanb-tanatanc

二倍角公式

tan2α=（2tanα）/（1-tan²α）

正切定理

Tan[正切]

在平面三角形中，正切定理說明任意兩條邊的和除以第一條邊減第二條邊的差所得的商等於這兩條邊的對角的和的一半的 正切除以第一條邊對角減第二條邊對角的差的一半的正切所得的商，即：

n倍角公式

tan(na)=sinna/cosna=∑（-1）（^i-1）/2×C(i)(n）×cos^n-i sin^i/∑（-1）^i/2×C(i)(n）×sin^n-i cos^i

例

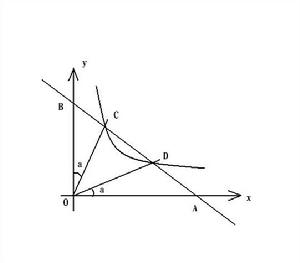三角函式例圖

這裡將為大家簡單敘述一下tan的三角函式公式。 如右圖。圖中用銳角符號表示出來的兩個角角度均為α。

則 tan α=1/3 的意思是

過C、D分別向y軸、x軸作垂線 （C、D為圖中的反比例函式與一條一般直線函式的交點，也為兩個 α 角非坐標軸的邊上的點）

構成含 α 角的直角三角形後，較短直角邊與較長直角邊的比為 1/3。

萬能公式

即使用tan(a/2)表示角a的三角函式（其中tan^2(a/2)=tan(a/2)*tan(a/2)）

sinα=（2tan(a/2)）/（1+tan^2(a/2)）

cosα=（1-tan^2(a/2)）/（1+tan^2(a/2)）

tanα=（2tan(a/2)）/（1-tan^2(a/2)）

cotα=（1-tan^2(a/2））/（2tan(a/2)）

secα=（1+tan^2(a/2)）/（1-tan^2(a/2)）

cscα=（1+tan^2(a/2)）/（2tan(a/2)）