基本介紹
設(a,b),[a,b](i=1,2,…,n;a,b∈R*)是R*中的區間,積集:
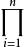 n維區間
n維區間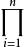 n維區間
n維區間(a,b)與 [a,b]
即n維空間中的集{x=(x,x₂,…,x)|a<x<b,i=1,2,…,n}與{x=(x₁,x₂,…,x)|a≤x≤b,i=1,2,…,n}分別稱為 n維開區間與 n維閉區間。
記為(a,b)與[a,b],其中a=(a,a,…,a),b=(b,b,…,b),(a,b)([a,b])稱為(a,b)([a,b])的支區間。若所有a,b是實數,則稱(a,b),[a,b]為 n維有界區間,否則稱為 n維無界區間,上述區間統稱為 n維區間。從幾何上看,二維有界區間就是矩形,三維有界區間就是長方體,因此,也把n維有界區間稱為n維長方體。特別地,當b-a=b-a=…=b-a時,又稱為n維方體或n維方區間。例如:
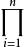 n維區間
n維區間(a-δ,a+δ)
就是n維開方區間,a=(a,a,…,a)稱為它的中心,2δ是它的棱長。n維區間(a,b)與[a,b]的n維體積是 :
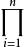 n維區間
n維區間(b-a)。
n維區間I的容積
 n維區間
n維區間n維區間 的容積都定義為:
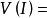 n維區間
n維區間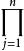 n維區間
n維區間(b-a), (1)
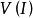 n維區間
n維區間 n維區間
n維區間 n維區間
n維區間 n維區間
n維區間於是,當n=1時, 即為一維區間 的長度,當n=2時, 即為平面矩形面積;當n=3時, 即為空間長方體的體積 。
下面我們講的R 的積分,一般都假定n≥2。
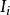 n維區間
n維區間如果R 內的點集S可以表為有限個無公共內點的n維區間 之並,即若
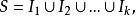 n維區間
n維區間我們便定義S的容積為
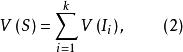 n維區間
n維區間我們約定由有限個無公共內點的n維區間所成之並集,簡單地說成是n-區間有限並集。
性質1 若S是Rⁿ的一個n-區間有限並集,則S的容積與組成S的這些區間的表示方法無關(圖1) 。
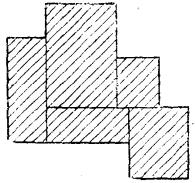 圖1
圖1 n維區間
n維區間 n維區間
n維區間證明 設S=∪ =∪J,其中 是有限個彼此無公共內點的閉區間,J也是有限個彼此無公共內點的閉區間。利用所有I與J的界面,將S分割為一系列彼此無公共內點的閉區間I'與一系列彼此無公共內點的閉區間J'。每個I'的成員與J'的每一個成員,或者無公共內點,或者內部完全重合,而所有I'的並集即為所有J'的並集。故有圖(2)
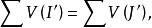 n維區間
n維區間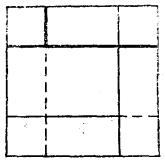 圖2
圖2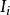 n維區間
n維區間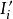 n維區間
n維區間另一方面,每個又是有限個之並;每個J又是有限個J'之並。 即
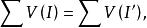 n維區間
n維區間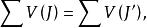 n維區間
n維區間所以
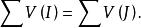 n維區間
n維區間 n維區間
n維區間性質2 如果S與T都是n維區間的有限並集,且TS,則:
V(S\T)=V(S) -V(T). (3)
證明因為(S\T)∪T=S,而S\T與T均為無公共內點的n維區間之並集。故由定義,有:
V(S\T)+V(T)=V(S),
此即(3)圖(3) 。
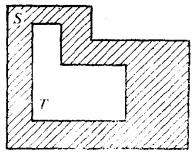 圖3
圖3性質3設S、T都是n-區間的有限並集,則有
V(S∪T)+V(S∩T)=V(S)+V(T). (4)
證明因為:SUT= [S\(S∩T)J∪[T\(S∩T)]∪[S∩T],
而S\(S∩T),T\(S∩T)和(S∩T)仍是n-區間的有限並集,它們彼此無公共內點,所以按定義,有
V(SUT)
=V[S\(S∩T)]+V[T\(S∩T)]+V(S∩T)
=V(S)-V(S∩T)+V(T)-V(S∩T)+V(S∩T)
=V(S)+V(T )-V(S∩T)
移項後,即為(4) (圖4) 。
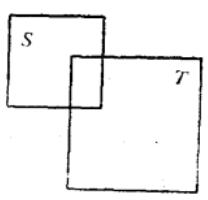 圖4
圖4