簡介
sin函式,即正弦函式,三角函式的一種。
數學術語
正弦函式是三角函式的一種
定義
 sin函式
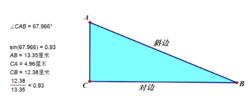
sin函式銳角正弦函式
在直角三角形ABC中,∠C是直角,AB是∠A斜邊,BC是∠A的對邊,AC是∠B的對邊。
正弦函式就是 sin(A)=a/c
sinA=∠A的對邊:斜邊
正弦函式
對於任意一個實數x都對應著唯一的角(弧度制中等於這個實數),而這個角又對應著唯一確定的正弦值sinx,這樣,對於任意一個實數x都有唯一確定的值sinx與它對應,按照這個對應法則所建立的函式,表示為y=sinx,叫做正弦函式。
單位圓定義
圖像中給出了用弧度度量的某個公共角。逆時針方向的度量是正角而順時針的度量是負角。設一個過原點的線,同 x軸正半部分得到一個角 θ,並與單位圓相交。這個交點的 y坐標等於 sin θ。在這個圖形中的三角形確保了這個公式;半徑等於斜邊並有長度 1,所以有了 sin θ= y/1。單位圓可以被認為是通過改變鄰邊和對邊的長度並保持斜邊等於 1 查看無限數目的三角形的一種方式。即sin θ=AB,與y軸正方向一樣時正,否則為負
對於大於 2π 或小於 0 的角度,簡單的繼續繞單位圓旋轉。在這種方式下,正弦變成了周期為 2π的周期函式。
基本性質
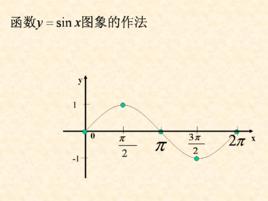
圖像
圖像是波形圖像(由單位圓投影到坐標系得出),叫做正弦曲線(sine curve)
定義域
實數集R
值域
[-1——1] (正弦函式有界性的體現)
最值和零點
①最大值:當x=2kπ+(π/2) ,k∈Z時,y(max)=1
②最小值:當x=2kπ+(3π/2),k∈Z時,y(min)=-1
零值點: (kπ,0) ,k∈Z
對稱性
1)對稱軸:關於直線x=(π/2)+kπ,k∈Z對稱
2)中心對稱:關於點(kπ,0),k∈Z對稱
周期性
最小正周期:2π
奇偶性
奇函式 (其圖象關於原點對稱)
單調性
在[-(π/2)+2kπ,(π/2)+2kπ],k∈Z上是增函式
在[(π/2)+2kπ,(3π/2)+2kπ],k∈Z上是減函式
正弦函式
正弦型函式解析式:y=Asin(ωx+φ)+b
各常數值對函式圖像的影響:
φ:決定波形與X軸位置關係或橫向移動距離(左加右減)
ω:決定周期(最小正周期T=2π/∣ω∣)
A:決定峰值(即縱向拉伸壓縮的倍數)
b:表示波形在Y軸的位置關係或縱向移動距離(上加下減)
作圖方法運用“五點法”作圖
“五點作圖法”即取當X分別取0,π/2,π,3π/2,2π時y的值。 [1]