SEC[正割]

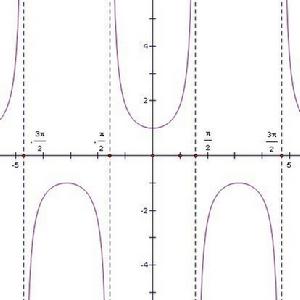
正割函式圖像

SEC[正割]

直角三角形斜邊與某個銳角的鄰邊的比,叫做該銳角的正割，用 sec（角）表示 。

SEC[正割]

正割與餘弦互為倒數，餘割與正弦互為倒數。即：

SEC[正割]

在 中，以x的任一使secθ有意義的值與它對應的y值作為(x，y)．在直角坐標系中作出的圖形叫正割函式的圖像，也叫正割曲線．

SEC[正割]

的性質：

(1)定義域,θ不能取90度,270度,-90度,-270度等值; 即 θ ≠kπ+π/2 或 θ≠kπ-π/2 (k∈Z）

(2)值域,|secθ|≥1．即secθ≥1或secθ≤－1;

SEC[正割]

(3) 是偶函式，即sec(－θ)=secθ．圖像對稱於y軸;

SEC[正割]

(4) 是周期函式．周期為2kπ(k∈Z，且k≠0)，最小正周期T=2π．