介紹
在分形幾何中, 計盒維數也稱為 盒維數、 閔可夫斯基維數,是一種測量距離空間( X, d)(特別是豪斯多夫空間)比如歐氏空間 R中分形維數的計算方法。
要計算分形 S的維數,你可以想像一下把這個分形放在一個均勻分割的格線上,數一數最小需要幾個格子來覆蓋這個分形。通過對格線的逐步精化,查看所需覆蓋數目的變化,從而計算出計盒維數。
假設當格子的邊長是 ε時,總共把空間分成 N個格子,那么計盒維數就是:
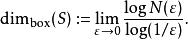 計盒維數
計盒維數當極限不收斂時,我們必須指出頂盒維數或底盒維數,或者說,計盒維數僅在和頂盒維數與底盒維數相等時才是有定義的。頂盒維數也稱為 能量維數、 科莫格洛夫維數、 科莫格洛夫容積,或者 閔可夫斯基上界維數,類似的可定義 閔可夫斯基下界維數。
計盒維數以及頂盒維數、底盒維數都和更常用的豪斯多夫維數有關,而且它們通常是一致的,只有在極特別的情況下才有區別。更詳細的區別參考下文。另一個分形維的度量是關聯維數。
定義的變化
盒子可以是方的,也可以是圓的,我們可以用半徑為 ε 的球來覆蓋空間,並逐步減小球的半徑。使用球的好處是,它比方形的數學形式更簡單,並且更容易套用到更一般的距離空間,而方形僅在歐幾里德空間中才有直觀的定義。
而使用方形的格子也有它的好處,在很多情況下方格的 N(ε) 計算更簡單,並且盒子的數目和它的覆蓋數是相等的,而同樣的覆蓋數,需要更多個球。
與豪斯多夫維數的關係
計盒維數是定義分形維的若干種方法之一。對於很多定義良好的分形來說,這些不同分數維的值是相等的。特別是當分型滿足開集條件時,這些維數一致。比如說,對康托集來說,它的豪斯多夫維數、底盒維數、頂盒維數都等於 log(2)/log(3)。然而它們的定義是不同的。
計盒維數和豪斯多夫維數存在如下不等式:
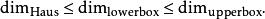 計盒維數
計盒維數一般的這兩個不等式可能是嚴格不等的。當分型在不同尺寸有著不同行為時,頂盒維數可能大於底盒維數。例如,驗證一下區間 [0,1] 中滿足以下條件的數集
對於任何 n, 所有在第 2位和第 2−1 位之間(含兩端)的數字均為 0
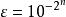 計盒維數
計盒維數在“奇位置區間”的數位沒有限制,例如,在第 2位和 2−1 位間的數字沒有限制,可以取任何值。該分型的頂盒維度為 2/3 而底盒維度為 1/3。這點很容易通過計算 N( ε) ()並注意到這些值在 n分別取奇數和偶數時表現不同來證實。
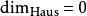 計盒維數
計盒維數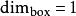 計盒維數
計盒維數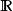 計盒維數
計盒維數更多例子:有理數集Q,是一可數集故而其 ,但是其因為其閉包的維度是 1 。實際上,
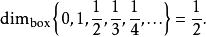 計盒維數
計盒維數這些例子顯示了增添可數集能改變計盒維度,揭示了這種維度的一種不穩定性。
參見
•不確定性係數
•關聯維數
•豪斯多夫維數
•空隙度
•填充維數
•Weyl-Berry 猜想
