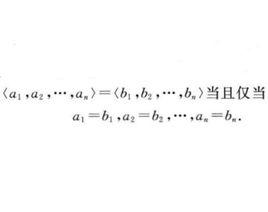定義
序偶兩個按一定次序排列的元素以與b組成一個有序序列稱為序偶或有序偶或有序二元組,並可記為(a,b),其中a與b分別稱為(a,b)的第一分量與第二分量。 注意:序偶構成了兩個元素間的次序,並構成了一種新的、特殊結構的元素,其本身並不表示由兩個元素所組成的集合。序偶的概念很重要,在客觀世界中我們經常會遇到序偶。
n元有序組 在序偶基礎上可以將其擴展至多個,而組成n元有序組,它可定義如下:
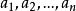 n元有序組
n元有序組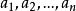 n元有序組
n元有序組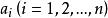 n元有序組
n元有序組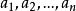 n元有序組
n元有序組n個按一定次序排列的元素 組成一個有序序列稱為n元有序組,並記為( )。其中 可稱為( )的第i個分量 。
舉例說明
例1 表示日期:年、月、日可用三元有序組表示:(年、月、日)。
例2 表示時間:時、分、秒可用三元有序組表示:(時、分、秒)。
例3 一個身份證號碼是由持有人的:省(自治區、直轄市)、市、區,出生年、月、日以及相應序列號和糾錯碼等八元有序組組成,它可表示為:
(省(自治區、直轄市)、市、區、年、月、日、序列號、糾錯碼)
例4 三維空間坐標繫上的點可用三元有序組(x,y,z)表示 。
n元有序組的性質
n元有序組有如下一些主要性質:
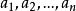 n元有序組
n元有序組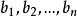 n元有序組
n元有序組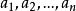 n元有序組
n元有序組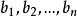 n元有序組
n元有序組n元有序組性質1:n元有序組( )與( )相等,即( )=( )的充分必要條件是:
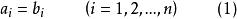 n元有序組
n元有序組n元有序組性質2:相同元素且不同次序所組成的n元有序組一般是不相等的 。
n元有序組集
概念
可以用n元有序組組成n元有序組集合。
n元有序組集:由n元有序組所組成的集合稱n元有序組集。
例5 每個人的籍貫:省、市、縣可以組成三元有序組:(省、市、縣),某公司職工全體的籍貫構成了一個三元有序組集合 。
n元有序組集與n階笛卡兒乘積
接下來,可以在n元有序組集合的基礎上構造n階笛卡兒乘積。
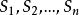 n元有序組
n元有序組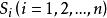 n元有序組
n元有序組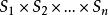 n元有序組
n元有序組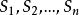 n元有序組
n元有序組定義 n階笛卡兒乘積:集合 將 中元素作為第i個分量構成的所有n元有序組形成n元有序組的過程稱n階笛卡兒乘積,可記為 ,其所形成的結果集C是一個n元有序組集,叫集合 的”階笛卡兒乘積,可表示為:
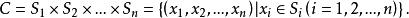 n元有序組
n元有序組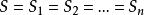 n元有序組
n元有序組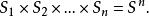 n元有序組
n元有序組當 時,n階笛卡爾乘積可簡記為S ,即