定義
設G是1,2,...,n 的置換群。若k是1…n中的某個元素,G中使k保持不變的置換的全體,記以Zk,叫做G中使k保持不動的置換類,簡稱k不動置換類 。
性質
群G中關於k的不動置換類Zk是G的一個子群。
證明
封閉性:p1,p2分別是使k不動的兩個置換,即p1,p2屬於Zk,則p1p2屬於Zk。
結合律:對於群結合律成立,Zk屬於G,故Zk中元素結合律成立。
單位元:群G的單位元屬於Zk,也是Z的單位元。
逆元素:p屬於Zk使得k保持不變,p的逆元屬於G也使k不變,故逆元存在。
因此Zk本身也是一個群,是群G的一個子群。
重要定理
G是S的一個子群,Z表示G中k不動的置換群。k所屬的等價類記為E。有
 k不動置換類
k不動置換類 k不動置換類
k不動置換類 k不動置換類
k不動置換類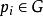 k不動置換類
k不動置換類 k不動置換類
k不動置換類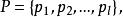 k不動置換類
k不動置換類 k不動置換類
k不動置換類證明:令k所在的等價類 ,且 由關係定義可知,存在 ,使得 令 構造
下面證明它們具有如下3個性質:
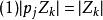 k不動置換類
k不動置換類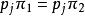 k不動置換類
k不動置換類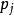 k不動置換類
k不動置換類 k不動置換類
k不動置換類 k不動置換類
k不動置換類 k不動置換類
k不動置換類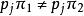 k不動置換類
k不動置換類 k不動置換類
k不動置換類假若 ,用 的逆元 左乘等式兩邊,推出 . 所以當 時,必有 .由此可知 .
 k不動置換類
k不動置換類 k不動置換類
k不動置換類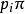 k不動置換類
k不動置換類 k不動置換類
k不動置換類 k不動置換類
k不動置換類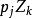 k不動置換類
k不動置換類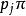 k不動置換類
k不動置換類 k不動置換類
k不動置換類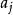 k不動置換類
k不動置換類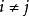 k不動置換類
k不動置換類 k不動置換類
k不動置換類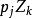 k不動置換類
k不動置換類中的任意元素 均把 映射到 , 中的任意元素, 均把 映射到 ,因為 ,所以 和 沒有公共元素。
 k不動置換類
k不動置換類 k不動置換類
k不動置換類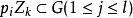 k不動置換類
k不動置換類 k不動置換類
k不動置換類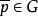 k不動置換類
k不動置換類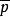 k不動置換類
k不動置換類 k不動置換類
k不動置換類 k不動置換類
k不動置換類因為 ,所以 . 由此得出 .另一方面,任取, 則是D上的置換,,則a與等價,
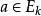 k不動置換類
k不動置換類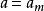 k不動置換類
k不動置換類 k不動置換類
k不動置換類 k不動置換類
k不動置換類故,不妨假設,由於,所以由此可知,
 k不動置換類
k不動置換類從而
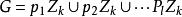 k不動置換類
k不動置換類.
由上述3個性質可以得到
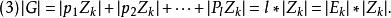 k不動置換類
k不動置換類 k不動置換類
k不動置換類 k不動置換類
k不動置換類 k不動置換類
k不動置換類例1.對於,有,滿足
例2:G={e, (12), (34), (12)(34) }
E=E={1, 2},Z=Z={e, (34) },|E| *|Z|=2*2=4=|G|.
套用
G={e, (1,2), (3,4), (1, 2)(3, 4)
則使1不動的置換類Z1={e, (3, 4)},其中e是單位元
設G是N={1,2,...,n}上的置換群,G在N上可以引出不同的等價類,則不同等價類的個數為
1.G={e, (1,2), (3,4), (1, 2)(3, 4)
則使1不動的置換類Z1={e, (3, 4)},其中e是單位元
2.設G是N={1,2,...,n}上的置換群,G在N上可以引出不同的等價類,則不同等價類的個數為
 k不動置換類
k不動置換類其中,| G | 表示群G中元素的個數。具體證明方法見:burnside引理
