多面體各個面
如圖所示:
 Szilassi多面體
Szilassi多面體 Szilassi多面體
Szilassi多面體 Szilassi多面體
Szilassi多面體 Szilassi多面體
Szilassi多面體旋轉透視圖
如圖所示:
 Szilassi多面體
Szilassi多面體頂點坐標
當一Szilassi多面體的最短邊長為一、重心位於原點時,此時14頂點分別為:
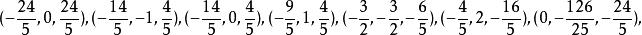 Szilassi多面體
Szilassi多面體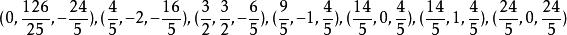 Szilassi多面體
Szilassi多面體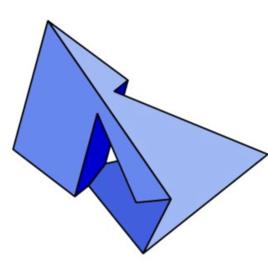
Szilassi多面體是一種凹多面體,是七面體的一種,拓撲結構的環,有7個六邊形面,其中有六個面是凹六邊形。 Szilassi多面體每個面都與相鄰的面共用邊。因此,可用七種顏色來塗滿每個相鄰的面,是七色定理的下限。 它有一個180度的對稱軸;它有3組面全等並留下一個未成對六邊形而構成的多面體。 Szilassi多面體的14個頂點和21個邊在一個環面嵌入Heawood graph的四面體和Szilassi的多面體是目前已知的兩個每個面都與其他面共邊的多面體。
如圖所示:
 Szilassi多面體
Szilassi多面體 Szilassi多面體
Szilassi多面體 Szilassi多面體
Szilassi多面體 Szilassi多面體
Szilassi多面體如圖所示:
 Szilassi多面體
Szilassi多面體當一Szilassi多面體的最短邊長為一、重心位於原點時,此時14頂點分別為:
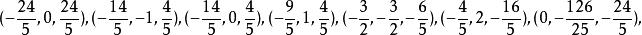 Szilassi多面體
Szilassi多面體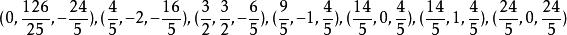 Szilassi多面體
Szilassi多面體