簡介
NL完全是由全體對NL類完備的語言構成的複雜性類。也就是說,NL完全的語言是NL類中最“難解”和最“有力”的語言。如果有某個確定性的方法可以在對數空間內解決一個NL完全問題,那么就會有NL=L。
定義
在全體判定問題中, NL類包含了那些可以用非確定型圖靈機在對數空間內解決的問題。這裡的圖靈機要求有一條唯讀輸入帶,和另一條空間上限與輸入長度的對數成比例的讀寫帶。類似地, L類包含了可以用同樣結構的確定型圖靈機解決的判定問題。由於這種圖靈機的格局數目只有多項式級別,因此 NL和 L都是 P的子集。
正式地說,一個問題是 NL完全的,若且唯若它屬於 NL,並且所有 NL中的判定問題都可以Log-空間規約到它。
NL
L是NL的子集, NL是可以被非確定型圖靈機利用對數空間解決的判定問題集合。利用薩維奇定理的建構式證明,可得證NL包含在複雜度P之內,也就是可以被確定型圖靈機在多項式空間解決的判定問題集合中。
存在幾個已知的 NL-完全問題,如2SAT。
根據薩維奇定理,我們已知有以下重要性質:
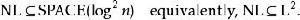 NL完全
NL完全計算複雜性理論
計算複雜性理論(Computational complexity theory)是理論計算機科學和數學的一個分支,它致力於將可計算問題根據它們本身的複雜性分類,以及將這些類別聯繫起來。一個可計算問題被認為是一個原則上可以用計算機解決的問題,亦即這個問題可以用一系列機械的數學步驟解決,例如算法。
如果一個問題的求解需要相當多的資源(無論用什麼算法),則被認為是難解的。計算複雜性理論通過引入數學計算模型來研究這些問題以及定量計算解決問題所需的資源(時間和空間),從而將資源的確定方法正式化了。其他複雜性測度同樣被運用,比如通信量(套用於通信複雜性),電路中門的數量(套用於電路複雜性)以及中央處理器的數量(套用於並行計算)。計算複雜性理論的一個作用就是確定一個能或不能被計算機求解的問題的所具有的實際限制。
在理論計算機科學領域,與此相關的概念有算法分析和可計算性理論。兩者之間一個關鍵的區別是前者致力於分析用一個確定的算法來求解一個問題所需的資源量,而後者則是在更廣泛意義上研究用所有可能的算法來解決相同問題。更精確地說,它嘗試將問題分成能或不能在現有的適當受限的資源條件下解決這兩類。相應地,在現有資源條件下的限制正是區分計算複雜性理論和可計算性理論的一個重要指標:後者關心的是何種問題原則上可以用算法解決。
