提問
對於任意一條線段AB,如何將它N等分呢?
根據平分線
這涉及到角平分線的一個性質。
作一條適當的線段CD(注意,是適當!!),作完後將它延長(N-1)倍為線段EF(這可以做到吧),再以A為圓心,CD的長為半徑作圓,記為⊙A(這可以做到):再以B為圓心,EF的長為半徑作圓,記為⊙B;⊙A與⊙B相交於點P再作∠P的角平分線,交線段AB於點Q,點Q為線段AB的N等分點。
根據三角形
這涉及到相似三角形的性質。
第一步:以AB中的任一點(就用A點)為頂點畫一條射線
第二步:用圓規取任意半徑,以射線頂點為圓心畫弧,與射線交點記做M1,再以該弧與射線的交點、以同樣半徑畫弧,重複N次。
第三步:連線B點和Mn點(最後一個交點)
第四步:過M1、M2……Mn-1做線段BMn的平行線,交點記做Q1、Q2、……、Qn-1,這些點都是線段AB的N等分點。
其他
1)線上段AB所在直線外取一點P,連線PA,PB 在PA上任取一點D,過D做AB的平行線,交PB於點C。
2)連線BD,AC,交點為E2,做射線PE2與AB交於F2,那么F2即為二等分點。
3)連線DF2交AC於點E3,做射線PE3與AB交於F3,那么F3為三等分點。
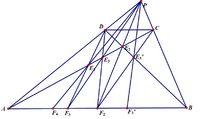 白郎松分法
白郎松分法4)依次能做出F4,F5……
