方法一：
過線段AB一端點做射線AO，依次截取三段等長線段AM MN NL，連線LB 過M N做平行與LB直線交AB與 X Y
X Y為等分點。
方法二：
將線段轉成一三角形的一條中線再畫做AB邊的中垂線（這步不用說明吧）交AB於M，連MC交AO於N（N即是ABC重心），AO=3NO。
方法三：
有一種佘氏尺規法。
方法四：
線段AB，過A點做直線與AB夾角為60度，作角平分線AC，角CAB為30度，過B作垂線交AC與C，平分角ACB交AB於D，則AB=√3CB，CB=√3DB，AB=3DB。
方法五：
已知線段AB，以AB為對角線作出平行四邊形ACBD，作AC邊與BD邊的中點E與F，連線DE與CF，可三等分AB（利用相似，其實做的練習中就有這樣的圖形）
方法六：
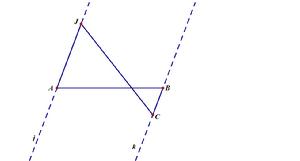
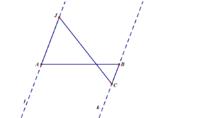相似方法做線段等分已知線段AB，過點A與B做一組不與AB重合平行線 j 與 k ，在k 上截取一點E，做為一倍長，在AB與E的異側直線 j 上，用尺規作圖截取2倍BE長度AF，連線FE可三等分AB。
在AB與E的異側直線 j 上，用尺規作圖截取n倍BE長度AF'，連線F'E可（n+1）等分AB。
針對三等分線段不要用這種很大眾的解決方法，這個N等分都沒關係的，沒有針對性
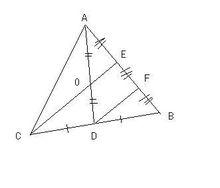三等分線段以分割AB三等分為列子
以AB為邊做一個三角形ABC
取BC中點D，連線AD
取AD中點O,連線CO並延長與AB相交於E
取BE中點F
這樣E、F就是AB的三等分點
這個可以被證明的，比做平行線要準的多，
方法七：
已知線段AB，作射線AP垂直於AB，
從點B開始，以3AB長為半徑畫弧，交AP於點C，連線BC。
∵BC=3AB，∴可以輕易得到BC的三等分點M'，N'。
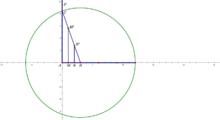三等分線段根據三角形相似原理，如果作M'M⊥AB，N'N⊥AB，那么M和N就是AB的三等分點
方法八：
1：以線段端點A為圓心，線段AB的長為半徑，作圓弧R。
2：將線段AB作二等份，求得線段AB的中點C。
3：作垂直於線段AB，且垂直於C點的直線Y；
4：直線Y與圓弧R相交，得交點T；
5：連線端點A，端點T，得線段AT；
6：連線端點B，端點T，得線段BT；
7：將線段AT作二等份，求得線段AT的中點D。
8：線接端點B，端點D，得線段BD；
9：將線段BT作二等份，求得線段BT的中點E。
10：線接端點E，端點A，得線段AE；
11：連線線段AT的中點D，線段AB的中點C，求得線段DC；
12：連線線段BT的中點E，線段AB的中點C，求得線段EC；
13：線段AE與線段DC相交，求得交點F；
14：線段BD與線段EC相交，求得交點G，
15：連線端點T，交點F，得線段TF，作線段TF延長線相交線段AB於交點h，
16：連線端點T，交點G，得線段TG，作線段TG延長線相交線段AB於交點k，
分別得線段Ah，hk，kB，為線段AB的三等份。
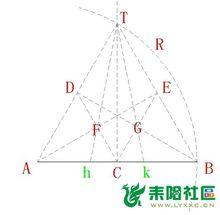三等分線段方法九：
利用等邊三角形的性質也能三等分線段。已知線段AB：
1：作直線j垂直於AB交點B。
2：作等邊三角形ABT（其實只需要∠TAB=60°即可）。
3：做角平分線平分∠CAB交直線j於點D。
4：以點A為圓心，線段AD為半徑做弧交直線j與另一點E。
5：連線AE，可證△ADE為等邊三角形。
6：作△ADE中AE中線交AB於F，BF是AB的三分之一。
