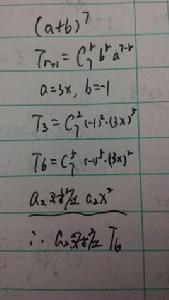推導過程
一、 由二次方看
首先，我們知道兩個數的二次方的計算方法
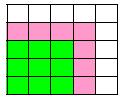N次方差公式已知一個數A的平方，求這個數相鄰數的平方。解答：如圖，一個數A的平方如圖中有色部分，即A^2；這個數的相鄰數的平方可以看圖中的白色方框包含的部分和綠色框線包含的部分，他們分別是：
5^2-4^2=5^(2-1)+4^(2-1)=5+4=9
幾何上可以理解為：圖中白色框的一邊5與另一邊4相加
4^2-3^2=4^(2-1)+3^(2-1)=4+3=7
幾何上可以理解為：圖中綠色框的一邊3與另一邊4的相加
所以對於相鄰兩數的二次方的差計算的一般公式如下：
(A+1)^2-A^2=(A+1)^(2-1)*A^(2-2)+(A+1)^(2-2)*A^(2-1)
對於最外邊白色框與裡邊綠色框的平方差，可通過圖形看到
(A+1)^2-（A-1)^2=(A+1)^(2-1)* (A-1)^(2-2)*2+(A+1)^(2-2)*(A-1)^(2-1)*2
=[(A+1)^(2-1)* (A-1)^(2-2)+(A+1)^(2-2)*(A-1)^(2-1)]*2
幾何上理解為：
長方向的A+1與[(A+1)-(A-1)]=2的面積、寬方向上A-1與[(A+1)-(A-1)]=2的面積，兩塊面積的和。
同理，推廣到兩個不相鄰數P與Q的平方差，可表示為：
P^2-Q^2=[P^(2-1)*Q^(2-2)+P^(2-2)*Q^(2-1)]*(P-Q)
二、 再看三次方的情況
我們看相鄰兩個數的三次方的差的計算方法：
已知一個數A的三次方，求這個數相鄰數的三次方。
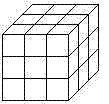N次方差公式設A的相鄰數為A+1和A-1，則他們的三次方可以用一個三維立體圖形形象地表示，如右圖：(A+1)^3-A^3=(A+1)^(3-1)*A^(3-3)+(A+1)^(3-2)*A^(3-2)+(A+1)^(3-3)*A^(3-1)
A^3-(A-1)^3=A^(3-1)*(A-1)^(3-3)+A^(3-2)*(A-1)^(3-2)+A^(3-3)*(A-1)^(3-1)
幾何上的理解是：
長方向的A與高方向上的A厚度為1的體積、寬方向上的（A-1）與高方向上的A厚度為1的體積、長方向上的（A-1）與寬方向上的（A-1）厚度為1的體積，這三塊體積之和。
對於不相鄰兩個數P、Q的三次方的差，可以看作是厚度為（P-Q）的形成體積的體積差，一般公式為：
P^3-Q^3=[P^(3-1)*Q^(3-3)+P^(3-2)*Q^(3-2)+P^(3-3)*Q^(3-1)]*(P-Q)
三、 推廣到四次方
同樣，可以知道相鄰兩個數的四次方之差公式：
(A+1)^4-A^4=(A+1)^(4-1)*A^(4-4)+(A+1)^(4-2)*A^(4-3)+(A+1)^(4-3)*A^(4-2)+(A+1)^(4-4)*A^(4-1)
不相鄰兩數的四次方之差的一般公式：
P^4-Q^4=[P^(4-1)*Q^(4-4)+P^(4-2)*Q^(4-3)+P^(4-3)*Q^(4-2)+P^(4-4)*Q^(4-1)]*(P-Q)
四、 結論：兩個數的n次方之差計算方法，
綜上，我們可以由簡單而複雜，推而廣之，得出
相鄰兩個數的n次方的差的一般公式：
P^n - Q^n=P^(n-1)*Q^(n-n)+P^(n-2)*Q^1+ P^(n-3)*Q^2+ P^(n-4)*Q^3+……+ P^(n-n)*Q^(n-1)
不相鄰兩個數的n次方的差的一般公式：
P^n - Q^n=[P^(n-1)*Q^(n-n)+P^(n-2)*Q^1+ P^(n-3)*Q^2+ P^(n-4)*Q^3+……+ P^(n-n)*Q^(n-1)]*(P-Q)
推廣到n次方
a^n-b^n=(a-b)(a^(n-1)+a^(n-2)*b+a^(n-3)*b^2+……+a^2*b^(n-3)+a*b^(n-2)+b^(n-1)) (n是整數)
a^n+b^n=(a+b)(a^(n-1)-a^(n-2)*b+a^(n-3)*b^2-……+a^2*b^(n-3)-a*b^(n-2)+b^(n-1)) (n是奇數）
驗證
⑴ 相鄰兩數的N次方的差的計算驗證
3^4-2^4=81-16=65
3^4-2^4=3^3*2^0 + 3^2*2^1 + 3^1*2^2 + 3^0*2^3=65
6^6-5^6=46656-15625=31031
6^6-5^6=6^5*5^0 + 6^4*5^1 + 6^3*5^2 + 6^2*5^3 + 6^1*5^4 + 6^0*5^5
=31031
⑵不相鄰兩數的N次方的計算驗證
10^5-5^5=10000-3125=96875
10^5-5^5=[10*10*10*10*1+10*10*10*5+10*10*5*5+10*5*5*5+5*5*5*5]*5
=[10000+5000+2500+1250+625]*5=19375*5=96875
11^6-9^6=1771561-531441=1240120
11^6-9^6=[11^5*1+11^4*9+11^3*9^2+11^2*9^3+11^1*9^4+1*9^5]*(11-9)
=[161051+131769+107811+88209+72171+59049]*2
=620060*2
=1240120
