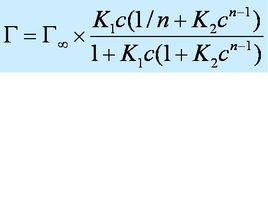定義
朗格繆爾的研究認為固體表面的原子或分子存在向外的剩餘價力,它可以捕捉氣體分子。這種剩餘價力的作用範圍與分子直徑相當,因此吸附劑表面只能發生單分子層吸附。
解題
所以,假定條件為:
① 吸附劑表面性質均一,每一個具有剩餘價力的表面分子或原子吸附一個氣體分子;
② 氣體分子在固體表面為單層吸附;
③ 吸附是動態的,被吸附分子受熱運動影響可以重新回到氣相;
④ 吸附過程類似於氣體的凝結過程,脫附類似於液體的蒸發過程。達到吸附平衡時,吸附速度等於脫附速度;
⑤ 氣體分子在固體表面的凝結速度正比於該組分的氣相分壓;
⑥ 吸附在固體表面的氣體分子之間無作用力。
設吸附劑表面覆蓋率為θ,則θ可以表示為:
θ=q/qm
式中:qm—吸附劑表面所有吸附點均被吸附質覆蓋時的吸附量,即飽和吸附量
氣體脫附速率與θ成正比,可以表示為kdθ,氣體的吸附速率與剩餘吸附面積(1-θ)和氣體分壓成正比,可以表示為kap(1-θ)。
吸附平衡時,吸附速率與脫附速率相等,則:
θ/(1-θ)=(ka/kd)p
式中:ka—吸附速率常數
kd—脫附速率常數
上式整理後,可得單分子層吸附的朗格繆爾(Langmuir)方程:
q=kpqm/(1+kp)
式中:k—Langmuir平衡常數,K=Ka/Kd.
Langmuir平衡常數k,與吸附劑和吸附質的性質以及溫度有關,其值越大,表示吸附劑的吸附性能越強。
該方程較好地描述了低、中壓力範圍的吸附等溫線。當氣體中吸附質分壓較高,接近飽和蒸汽壓時,該方程產生偏差。這是由於這時的吸附質可以在微細的毛細管中冷凝,單分子層吸附的假設不成立的緣故。