LCIS

定義

最長公共上升子序列，就是指，如果一個上升序列c∈序列a且c∈序列b。那么所有符合條件的序列c中最長的序列即是序列a和序列b的最長公共上升子序列。例如，序列2213和序列2123的LCIS為2 3，長度為2。

解析

算法：線性DP。

變數聲明：兩個字元串為a和b，長度分別為r1和r2

初始方法

狀態表示：f[i,j]表示字元串a、b中以a[i]、b[j]為結尾的最長公共上升子序列。

轉移方程：

當a[i]==b[j]時，f[i,j]=max(f[k,l])(0<k<i,0<l<j,a[k]==a[l],a[k]<a[i],a[l]<a[j])

否則 f[i][j]

目標：max(f[i,j])(0<i<=r1,0<j<=r2)

時間複雜度：O(r1*r2*r1*r2)（四重循環）

空間複雜度：r1*r2（二維）

評析：時間複雜度、空間複雜度過高，不建議使用。

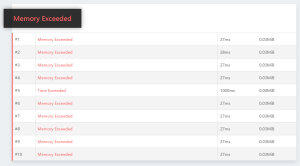原始方法評測情況原始方法評測情況

時間最佳化

一級最佳化

思路：我們發現之所以要每次都遍歷求解就是因為每個狀態保存的都是當前解而不是最優解。之所以每次都保存當前解，又是因為要將當前的狀態和之前的狀態進行比較，使得a[k]<a[i],b[l]<b[j]，從而保持單調上升的特性。但是我們可以發現，當我們需要遍歷之前的解時，a[i]==b[j]那么此時，僅僅需要知道a[i]，b[j]就可以直接得到。所以我們就可以記錄一個為當前狀態，而另一個為最優解，就可以每次求解時只遍歷一維了。

狀態表示：f[i,j]表示字元串a的前i個字元、b的前j個字元中以b[j]為結尾的最長公共上升子序列。

轉移方程：

當a[i]==b[j]時，f[i,j]=max(f[i-1,k])(0<k<j,b[k]<a[i])

否則f[i,j]=f[i-1,j]

目標：max(f[r1][j])(0<j<r2)

時間複雜度：O(r1*r2*r2)（三重循環）

空間複雜度：r1*r2(二維)

二級最佳化

思路：我們發現雖然算法已經最佳化了1維，但是每次求解時依然需要遍歷。在轉移過程中，我們把滿足0<k<j,b[k]<a[i]的k構成的集合稱為f[i,j]的進行狀態轉移時的決策集合，記為best(i,j)。注意到，在第二層循環j從1增加到r2的過程中，第一層循環的i是一個定值，這使得b[k]<a[i]是固定成立的。所以，當b[j]<a[i]滿足時，就用f[i,j]更新集合best。求解時，就可以直接用集合best得到答案。

狀態表示:f[i,j]表示字元串a的前i個字元、b的前j個字元中以b[j]為結尾的最長公共上升子序列。

轉移方程：

當a[i]==b[j]時，f[i,j]=best+1

否則f[i,j]=f[i-1,j];

目標：max(f[r1][j])(0<j<r2)

時間複雜度：O(r1*r2)（兩重循環）

空間複雜度：r1*r2（二維）

評析：時間複雜度上已經較為最佳化，但空間複雜度還有待最佳化。

空間最佳化

思路：滾輪最佳化，首先將i==1時所有的f[i,j]算出並存到f[0]數組中。然後將i==2時所有的f[i,j]算出來存到f[1]數組中，此時f[0]數組中的值已經不需要了，於是用f[1]中的值將其覆蓋掉。將i==3時所有的f[i,j]算出來存到f[1]數組中，此時f[0]數組中的值已經不需要了，於是用f[1]中的值將其覆蓋掉。將i==4時……然後將i==r1時所有的f[i,j]算出來存到f[1]數組中，此時f[0]數組中的值已經不需要了，於是用f[1]中的值將其覆蓋掉。最後將f[0]數組當做f[r1]數組使用即可。

狀態表示:f[1,j]表示字元串a的前i個字元、b的前j個字元中以b[j]為結尾的最長公共上升子序列。

轉移方程：當a[i]==b[j]時，f[1,j]=best+1
否則f[1,j]=f[0,j];
目標：max(f[1][j])(0<j<r2)
時間複雜度：O(r1*r2)（兩重循環）
空間複雜度：2*r2（近似於一維）
評析：時間複雜度、空間複雜度上都非常最佳化，推薦使用。

代碼

C++語言

​1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34		 ​#include<memory.h>
constintLCIS__r=3001;
longlongLCIS__f[LCIS__r][LCIS__r];
boolgreater(intx,inty)
{
returnx>y;
}
longlongbigger(longlongx,longlongy)
{
returnx>y?x:y;
}
template<typenamename>intLCIS(name*a,name*b,intl1,intr1,intl2,intr2,boolcompare(namex,namey))
{
longlongmaximum;
intnum=(r2+1)*sizeof(name);
for(inti=l2;i<=r2;i++)
if(b[i]==a[1])
for(;i<=r2;i++)LCIS__f[0][i]=1;
elseLCIS__f[0][i]=0;
for(inti=l1+1,j;i<=r1;i++)
{
for(maximum=0,j=l2;j<=r2;j++)
if(a[i]==b[j])LCIS__f[1][j]=maximum+1;
else
{
LCIS__f[1][j]=LCIS__f[0][j];
if(compare(a[i],b[j]))maximum=bigger(maximum,LCIS__f[1][j]);
}
memcpy(LCIS__f[0],LCIS__f[1],num);
}
for(inti=l2;i<=r2;i++)
maximum=bigger(maximum,LCIS__f[0][i]);
returnmaximum;
}

相關詞條

熱門詞條

聯絡我們