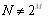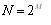FFT原理

FFT基本原理FFT是一種DFT的高效算法，稱為快速傅立葉變換（fast sform）。 從DFT運算開始，說明FFT的基本原理。

FFT基本原理

FFT是一種DFT的高效算法，稱為快速傅立葉變換（fast Fourier transform）。FFT算法可分為按時間抽取算法和按頻率抽取算法，先簡要介紹FFT的基本原理。從DFT運算開始，說明FFT的基本原理。
DFT的運算為：

式中

。
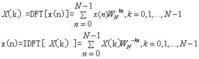
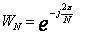
由這種方法計算DFT對於X（K）的每個K值，需要進行4N次實數相乘和（4N-2）次相加，對於N個k值，共需N*N乘和N（4N-2）次實數相加。改進DFT算法，減小它的運算量，利用DFT中

的周期性和對稱性，使整個DFT的計算變成一系列疊代運算，可大幅度提高運算過程和運算量，這就是FFT的基本思想。

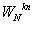
時間抽取（DIT）基2FFT算法

設N點序列x(n),
N=

,將x(n)按奇偶分組，有

，
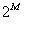
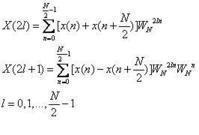
改寫為：

。
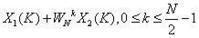
一個N點DFT分解為兩個 N/2點的DFT，

繼續分解，疊代下去，其運算量約為

。

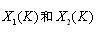
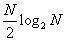
頻率抽取（DIF）2FFT算法

頻率抽取2FFT算法是按頻率進行抽取的算法。設N=

，
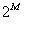
將x(n)按前後兩部分進行分解，

按K的奇偶分為兩組，即

得到兩個N/2 點的DFT運算。如此分解，并迭代，總的計算量和時間抽取（DIT）基2FFT算法相同。

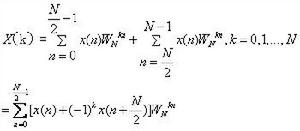
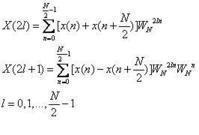
任意整數的FFT

時，可採取補零使其成為

，或者先分解為兩個p,q的序列，其中p+q=N，然後進行計算。