定義
經濟訂貨批量模型又稱整批間隔進貨模型EOQ模型，英文為，該模型適用於整批間隔進貨、不允許缺貨的存儲問題，即某種物資單位時間的需求量為常D，存儲量以單位時間消耗數量D的速度逐漸下降，經過時間T後，存儲量下降到零，此時開始定貨並隨即到貨，庫存量由零上升為最高庫存量Q，然後開始下—個存儲周期，形成多周期存儲模型。
經濟訂貨量基本模型的假設
1、企業能夠及時的補充存貨，即需要訂貨時便可以立即取得存活；
2、能集中到貨，而不是陸續入庫；
3、不允許缺貨，即無缺貨成本（TCs=0），這是因為良好的存貨管理本來就不應該出現缺貨成本；
4、需求量穩定，並且能預測，即D為已知常量；
5、存貨單價不變，即U為已知常量；
6、存貨現金充足，不會因為出現現金短缺而影響進貨；
7、所需存貨市場供應充足，不會因為買不到需要的存活而影響其他。
經濟訂貨量基本模型的推導
存貨成本構成
與存貨成本有關的，有如下三種即：取得成本、儲存成本和缺貨成本。
取得成本分為訂貨成本和購置成本。
A、訂貨成本：訂貨成本根據是否與訂貨次數有關，分成兩部分：第一，訂貨的固定成本，諸如常設採購機構的基本開支，這一部分我們用F1表示；第二，訂貨的變動成本，諸如差旅費、郵費等等，這一部分與訂貨次數有關，我們假設每一次的變動成本為K，存貨年需求量為D，每次進貨量為Q，把訂貨次數定義為D與Q的商，所以綜上，有公式如下：
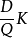EOQ模型訂貨成本=F1+
；其中，F1為固定成本、D為存貨年需求量、Q為每次進貨量、K為每一次的變動成本。
B、購置成本，即存貨本身的價值，由數量和單價決定，我們假設，單價為U，年需求量為D，則以DU表示購置成本。
所以，根據以上，有如下公式：
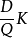EOQ模型TCa=F1+
+DU；
其中，TCa是取得成本，F1為固定成本、D為存貨年需求量、Q為每次進貨量、K為每一次的變動成本，DU為購置成本。
儲存成本是指為保持存貨而發生的費用，包括存貨占用資金所應計的利息、倉庫費用、保險費用等等。儲存成本根據是否與存貨數量有關，分成固定成本和變動成本。
A、固定成本，諸如倉庫人員工資等，用F2表示。
B、變動成本，諸如應計利息、保險費等，假定以Kc作為單位成本。
綜上，公式如下：
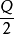EOQ模型TCc=F2+Kc
；
其中，TCc是儲存成本，F2是固定成本，Q為存貨量。
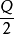EOQ模型註：之所以取
，是基於一個統計學上的考慮。假定一個存貨周期裡面，最多的存貨量為Q，最少的存貨量為0，我們知道，時點指標是不能相加的，而時期指標是可以相加的，要想使時點指標得以相加，常見的做法是取平均數，使時點指標變成時期指標。所以，我們取
作為可以相加減的時期數據代入公式進行計算。
缺貨成本定義為因為中斷而造成的損失，諸如停工損失，緊急外購成本等。
假定，總成本為TC，而且總成本構成由上面三個部分構成，於是有下面的公式：
TC=TCa+TCc+TCs
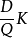EOQ模型=F1+
+DU+F2+Kc
+TCs
經濟訂貨量基本模型的推導
依據EOQ模型的基本假設，我們有如下的基本公式：
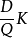EOQ模型TC=F1+
+DU+F2+Kc
令F1、K、D、F2、Kc為常數量，TC的大小取決於Q，為了求得TCmin，對其進行求導演算：
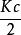EOQ模型TC′=
－
令TC′=0
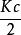EOQ模型有
=
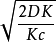EOQ模型有Q*=
上面的Q*公式即為經濟訂貨量基本模型
。
此外，還有如下的公式演變
：
每次最佳訂貨次數：
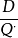EOQ模型N*=
=
=
與批量有關的存貨總成本：
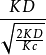EOQ模型TC（Q*）=
+
×Kc=
最佳訂貨周期：
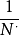EOQ模型t*=
=
經濟訂貨量占用資金：
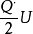EOQ模型I*=
=
經濟訂貨量基本模型的舉例
某企業每年消耗某種材料3600千克，該材料單位成本為10元，單位儲存成本為2元，一次訂貨成本為25元，則有如下
：
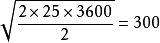EOQ模型Q*=
（千克）
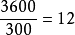EOQ模型N*=
（次）
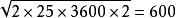EOQ模型TC（Q*）=
（元）
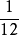EOQ模型t*=
（年）
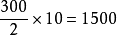EOQ模型I*=
（元）
