歷史
Yefim Dinitz在Adel'son-Vel'sky(AVL樹的發明者之一)的算法課的課前活動上發明了這個算法。當時他不知道關於Ford–Fulkerson算法的基本事實。
Dinitz在1969年一月向他人公布了他發明的算法,又在1970年將其發布在 Doklady Akademii nauk SSSR雜誌上。 在1974年,Shimon Even和(他之後的博士學生)Alon Itai在海法的以色列理工學院對Dinitz的算法以及Alexander Karzanov的阻塞流的想法很感興趣。但是雜誌上的文章每篇的篇幅被限制在四頁以內,很多細節都被忽略,這導致他們很難根據文章還原出算法。但他們沒有放棄,在後三天不斷地努力,設法了解這兩個檔案中的分層網路的維護問題。 在接下來的幾年,Even由於在講學中將Dinitz念為Dinic,導致Dinic算法反而成為了它的名稱。 Even和Itai也將算法與BFS和DFS結合起來,形成了當前版本的算法。
在Ford–Fulkerson算法被發明之後的約十年之內,使算法能在多項式複雜度之內處理不合理的邊界的方法是未知的。這造成缺乏任何已知的多項式複雜度算法解決最大流問題。 Dinitz算法和Edmonds–Karp算法在1972年發布,證明在Ford–Fulkerson算法中,如果每次總選擇最短的一條增廣路,路徑長度將單調增加,且算法總能終止。
算法介紹
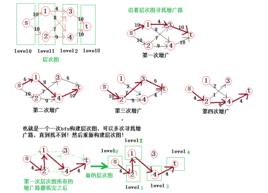
層次圖
層次圖,就是把原圖中的點按照點到源的距離分“層”,只保留不同層之間的邊的圖。
算法流程
1、根據殘量網路計算層次圖。
2、在層次圖中使用DFS進行增廣直到不存在增廣路。
3、重複以上步驟直到無法增廣。
時間複雜度
因為在Dinic的執行過程中,每次重新分層,匯點所在的層次是嚴格遞增的,而n個點的層次圖最多有n層,所以最多重新分層n次。在同一個層次圖中,因為每條增廣路都有一個瓶頸,而兩次增廣的瓶頸不可能相同,所以增廣路最多m條。搜尋每一條增廣路時,前進和回溯都最多n次,所以這兩者造成的時間複雜度是O(nm);而沿著同一條邊(i,j)不可能枚舉兩次,因為第一次枚舉時要么這條邊的容量已經用盡,要么點j到匯不存在通路從而可將其從這一層次圖中刪除。綜上所述,Dinic算法時間複雜度的理論上界是O(n^2*m)。
代碼實現
遞歸實現
代碼簡短,效率略低。(不是dinic,是最短路徑增值)
非遞歸實現
PASCAL代碼實現